题目内容
如图1是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》由四个全等的直角三角形和一个小正方形的拼成的大正方形.(1)如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是
(2)(2009年贵州省安顺市)若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是
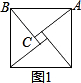

分析:(1)大正方形的面积即a2+b2.小正方形的面积是(b-a)2.已知这两个式子的值,根据变形就可求解;
(2)如图,根据勾股定理即可求得:BD,AD的长,即可求解.
(2)如图,根据勾股定理即可求得:BD,AD的长,即可求解.
解答:解:(1)大正方形的面积即a2+b2=13;小正方形的面积是(b-a)2=a2+b2-2ab=1,即13-2ab=1.解得:2ab=12.
∴(a+b)2=a2+b2+2ab=13+12=25;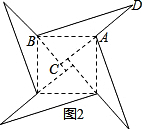
(2)在直角△BCD中:BD=
=
=13.
∴风车的外围周长=4BD+4AD=4×13+4×6=76.
∴(a+b)2=a2+b2+2ab=13+12=25;

(2)在直角△BCD中:BD=
| BC2+CD2 |
| 52+122 |
∴风车的外围周长=4BD+4AD=4×13+4×6=76.
点评:正确理解正方形的面积与直角三角形的边长之间的关系,是解决本题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目

 如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形的两直角边为a、b,则a+b的值等于
如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形的两直角边为a、b,则a+b的值等于 21、如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两条直角边的长分别为
21、如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两条直角边的长分别为 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.若图中大小正方形的面积分别为
如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.若图中大小正方形的面积分别为 10、如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则(a-b)(a2+b2)的值等于
10、如图,是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则(a-b)(a2+b2)的值等于