题目内容
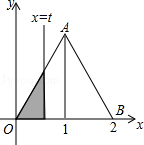
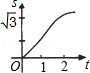
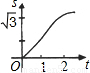
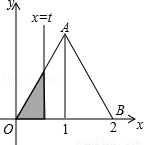
 如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )分析:等边△AOB中,l∥y轴,所以很容易求得∠OCB=30°;进而证明OD=t,CD=
t;最后根据三角形的面积公式,解答出S与t之间的函数关系式,由函数解析式来选择图象.
| 3 |
解答:解:①∵l∥y轴,△AOB为等边三角形,
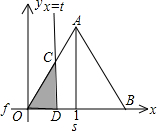
∴∠OCB=30°,
∴OD=t,CD=
t;
∴S△OCD=
×OD×CD
=
t2(0≤t≤1),
即S=
t2(0≤t≤1).
故S与t之间的函数关系的图象应为定义域为[0,1]、开口向上的二次函数图象;
②∵l∥y轴,△AOB为等边三角形
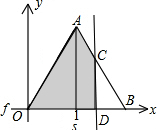
∴∠CBD=30°,
∴BD=2-t,CD=
(2-t);
∴S△BCD=
×BD×CD
=
(2-t)2(0≤t≤1),
即S=
-
(2-t)2(0≤t≤1).
故S与t之间的函数关系的图象应为定义域为[1,2]、开口向下的二次函数图象;
故选C.

∴∠OCB=30°,
∴OD=t,CD=
| 3 |
∴S△OCD=
| 1 |
| 2 |
=
| ||
| 2 |
即S=
| ||
| 2 |
故S与t之间的函数关系的图象应为定义域为[0,1]、开口向上的二次函数图象;
②∵l∥y轴,△AOB为等边三角形

∴∠CBD=30°,
∴BD=2-t,CD=
| 3 |
∴S△BCD=
| 1 |
| 2 |
=
| ||
| 2 |
即S=
| 3 |
| ||
| 2 |
故S与t之间的函数关系的图象应为定义域为[1,2]、开口向下的二次函数图象;
故选C.
点评:本题主要考查的是二次函数解析式的求法及二次函数的图象特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







 B.
B. C.
C. D.
D.