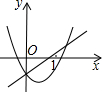
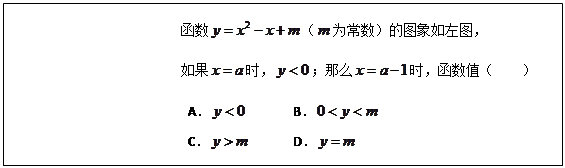题目内容
如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.

(1)设矩形的一边为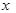 (m),面积为
(m),面积为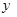 (m2),求
(m2),求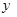 关于
关于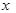 的函数关系式,并写出自变量
的函数关系式,并写出自变量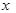 的取值范围;
的取值范围;
(2)当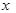 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?

(1)设矩形的一边为
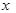 (m),面积为
(m),面积为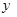 (m2),求
(m2),求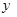 关于
关于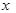 的函数关系式,并写出自变量
的函数关系式,并写出自变量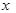 的取值范围;
的取值范围;(2)当
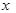 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?(1)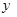 =
= ,0<
,0<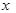 <18(2)9,81
<18(2)9,81
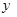 =
= ,0<
,0<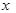 <18(2)9,81
<18(2)9,81解:(1) 由已知,矩形的另一边长为
 …………………………1分
…………………………1分
则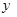 =
=  ……………………………………………3分
……………………………………………3分
= …………………………………5分
…………………………………5分
自变量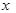 的取值范围是0<
的取值范围是0<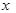 <18. ……………………………7分
<18. ……………………………7分
(2)∵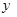 =
= =
= …………………10分
…………………10分
∴ 当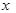 =9时(0<9<18),苗圃的面积最大 …………………11分
=9时(0<9<18),苗圃的面积最大 …………………11分
最大面积是81 …………………………………………12分
…………………………………………12分
又解: ∵ =-1<0,
=-1<0,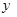 有最大值, ……………………8分
有最大值, ……………………8分
∴ 当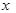 =
= 时(0<9<18),………………10分
时(0<9<18),………………10分
 (
( ) …………12分(未指出0<9<18暂不扣分)
) …………12分(未指出0<9<18暂不扣分)
(1)篱笆只有两边,且其和为18,设一边为x,则另一边为(18-x),根据公式表示面积;据实际意义,0<x<18;
(2)根据函数性质求最值,可用公式法或配方法.

 …………………………1分
…………………………1分则
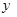 =
=  ……………………………………………3分
……………………………………………3分=
 …………………………………5分
…………………………………5分自变量
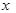 的取值范围是0<
的取值范围是0<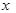 <18. ……………………………7分
<18. ……………………………7分(2)∵
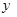 =
= =
= …………………10分
…………………10分∴ 当
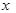 =9时(0<9<18),苗圃的面积最大 …………………11分
=9时(0<9<18),苗圃的面积最大 …………………11分最大面积是81
 …………………………………………12分
…………………………………………12分又解: ∵
 =-1<0,
=-1<0,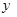 有最大值, ……………………8分
有最大值, ……………………8分∴ 当
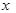 =
= 时(0<9<18),………………10分
时(0<9<18),………………10分 (
( ) …………12分(未指出0<9<18暂不扣分)
) …………12分(未指出0<9<18暂不扣分)(1)篱笆只有两边,且其和为18,设一边为x,则另一边为(18-x),根据公式表示面积;据实际意义,0<x<18;
(2)根据函数性质求最值,可用公式法或配方法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 的y与x的部分对应值如下表:
的y与x的部分对应值如下表: 的正根在3与4之间
的正根在3与4之间 的图象如图所示,则
的图象如图所示,则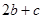 的值是( )
的值是( )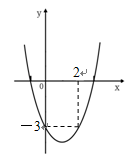
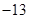
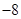
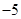
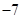
 。
。 ,下列说法正确的是( )
,下列说法正确的是( )

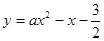 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.