题目内容
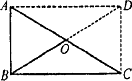
 如图,P是矩形ABCD内一点,PA=3,PD=4,PC=5,则PB为
如图,P是矩形ABCD内一点,PA=3,PD=4,PC=5,则PB为
- A.4.5
- B.

- C.
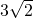
- D.4
C
分析:可过P作AB的平行线分别交DA、BC于E、F,过P作BC的平行线分别交AB、CD于G、H,如下图所示,将矩形ABCD分割成几个小矩形,利用勾股定理进行求解,进而得出结论.
解答: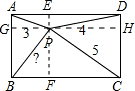 解:过P作AB的平行线分别交DA、BC于E、F,过P作BC的平行线分别交AB、CD于G、H.
解:过P作AB的平行线分别交DA、BC于E、F,过P作BC的平行线分别交AB、CD于G、H.
设AG=DH=a,BG=CH=b,AE=BF=c,DE=CF=d,
则 AP2=a2+c2,CP2=b2+d2,BP2=b2+c2,DP2=d2+a2,
于是AP2+CP2=BP2+DP2,
又因为PA=3,PD=4,PC=5,
故PB2=AP2+CP2-PD2=32+52-42=18,
则PB=3 .
.
故选C.
点评:本题主要考查了矩形的性质及勾股定理的运用,能够熟练运用勾股定理求解一些简单的计算问题.
分析:可过P作AB的平行线分别交DA、BC于E、F,过P作BC的平行线分别交AB、CD于G、H,如下图所示,将矩形ABCD分割成几个小矩形,利用勾股定理进行求解,进而得出结论.
解答:
 解:过P作AB的平行线分别交DA、BC于E、F,过P作BC的平行线分别交AB、CD于G、H.
解:过P作AB的平行线分别交DA、BC于E、F,过P作BC的平行线分别交AB、CD于G、H.设AG=DH=a,BG=CH=b,AE=BF=c,DE=CF=d,
则 AP2=a2+c2,CP2=b2+d2,BP2=b2+c2,DP2=d2+a2,
于是AP2+CP2=BP2+DP2,
又因为PA=3,PD=4,PC=5,
故PB2=AP2+CP2-PD2=32+52-42=18,
则PB=3
 .
.故选C.
点评:本题主要考查了矩形的性质及勾股定理的运用,能够熟练运用勾股定理求解一些简单的计算问题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
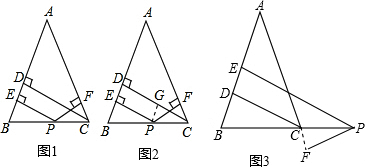
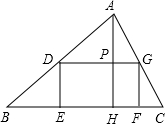
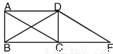
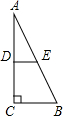 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )