题目内容
如图所示,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH为BC边上的高,AH交DG于点P,已知AH=3,BC=5;(1)设DG的长为x,矩形DEFG面积为y,求y关于x的函数解析式及其定义域;
(2)根据(1)中所得y关于x的函数图象,求当矩形DEFG面积最大时,DG的长为多少?矩形DEFG面积是多少?
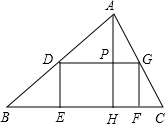
分析:(1)易证得△ADG∽△ABC,那么它们的对应边和对应高的比相等,可据此求出AP的表达式,进而可求出PH即DE、GF的长,已知矩形的长和宽,即可根据矩形的面积公式得到y、x的函数关系式;
(2)根据(1)题所得函数的性质及自变量的取值范围,即可求出矩形的最大面积及对应的DG的长.
(2)根据(1)题所得函数的性质及自变量的取值范围,即可求出矩形的最大面积及对应的DG的长.
解答:解:(1)∵矩形DEFG的边EF在△ABC的边BC上,
∴DG∥BC,(1分)
∴△ADG∽△ABC(2分)
∵AH⊥BC,
∴AP⊥DG
∴
=
,
∴
=
,(2分)
∴AP=
x,DE=PH=3-
x(1分)
∴y=-
x2+3x(0<x<5);(2分)
(2)y=-
x2+3x=-
(x-
)2+
;(1分)
根据函数图象可知,抛物线y=-
x2+3x开口向下,抛物线的顶点坐标是它的最高点,且x=
在函数的定义域内;(1分)
所以当DG的长为
时,矩形DEFG面积最大为
.(2分)
∴DG∥BC,(1分)
∴△ADG∽△ABC(2分)
∵AH⊥BC,
∴AP⊥DG
∴
| AP |
| AH |
| DG |
| BC |
∴
| AP |
| 3 |
| x |
| 5 |
∴AP=
| 3 |
| 5 |
| 3 |
| 5 |
∴y=-
| 3 |
| 5 |
(2)y=-
| 3 |
| 5 |
| 3 |
| 5 |
| 5 |
| 2 |
| 15 |
| 4 |
根据函数图象可知,抛物线y=-
| 3 |
| 5 |
| 5 |
| 2 |
所以当DG的长为
| 5 |
| 2 |
| 15 |
| 4 |
点评:此题主要考查了矩形的性质、相似三角形的判定和性质以及二次函数的应用等知识,能够根据相似三角形求出矩形的宽是解答此题的关键.

练习册系列答案
相关题目
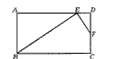
 如图所示,把矩形纸片ABCD,沿EF对折,若∠BFG=40°,则∠DEF=
如图所示,把矩形纸片ABCD,沿EF对折,若∠BFG=40°,则∠DEF=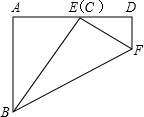 在一次数学课上,小明同学把一个长为6(AD=6)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的宽AB.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
在一次数学课上,小明同学把一个长为6(AD=6)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的宽AB.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)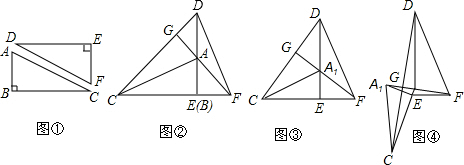
 在一次数学课上,小明同学把一个长为6(AD=6)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的宽AB.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
在一次数学课上,小明同学把一个长为6(AD=6)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的宽AB.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)