题目内容
已知平行四边形ABCD四个顶点到动直线l的距离分别为a、b、c、d,
(1)如图①,当直线l在平行四边形ABCD外时,证明:a+c=b+d;
(2)当直线l移动至与平行四边形ABCD相交(l与边不平行)时,上述关系还成立吗?若成立,试给予证明,若不成立,试找出a、b、c、d之间的关系,并给予证明.

(1)如图①,当直线l在平行四边形ABCD外时,证明:a+c=b+d;
(2)当直线l移动至与平行四边形ABCD相交(l与边不平行)时,上述关系还成立吗?若成立,试给予证明,若不成立,试找出a、b、c、d之间的关系,并给予证明.

(1)如图所示,连AC,BD相交于点O,过点O作OP⊥L于P,
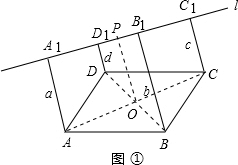
由题意可得,OP为AA1CC1的中位线,∴a+c=2OP,
同理,b+d=2OP,∴a+c=b+d.
(2)当直线l移动至与平行四边形ABCD相交时,上述关系不成立,以下几种情况说明:
①当四个顶点中一个顶点在直线的一侧(不妨设是D)而另外三个顶点在另一侧,则有b=a+c+d.
证明:如图所示,

由(1)可知,a+c=2OP,连DB1,过点O作OP⊥L于P,交DB1于Q,
则OQ为△DBB1的中位线,故OQ=
=
,同理,PQ=
,
所以OP=OQ-PQ=
-
,即,b-d=2OP,
所以a+c=b-d
即b=a+c+d.
②当有两个顶点在一侧(不妨设A,D),另外两个顶点在另一侧,则有a+b=c+d.
证明:如图所示,在①中有b-d=2OP,连接AC1,延长OP交AC1于R,

则PR为△AA1C1的中位线,故PR=
=
,同理,OR=
,所以OP=OR-PR=
-
,即c-a=2OP,
所以,c-a=b-d,
即a+b=c+d.
③当直线只过某一顶点,(设过顶点A,点D在直线的一侧,B,C在直线的另一侧)则b=d+2c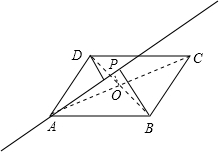
④当直线与对角线重合时(不妨设是AC)则b=d.


由题意可得,OP为AA1CC1的中位线,∴a+c=2OP,
同理,b+d=2OP,∴a+c=b+d.
(2)当直线l移动至与平行四边形ABCD相交时,上述关系不成立,以下几种情况说明:
①当四个顶点中一个顶点在直线的一侧(不妨设是D)而另外三个顶点在另一侧,则有b=a+c+d.
证明:如图所示,

由(1)可知,a+c=2OP,连DB1,过点O作OP⊥L于P,交DB1于Q,
则OQ为△DBB1的中位线,故OQ=
| BB1 |
| 2 |
| b |
| 2 |
| d |
| 2 |
所以OP=OQ-PQ=
| b |
| 2 |
| d |
| 2 |
所以a+c=b-d
即b=a+c+d.
②当有两个顶点在一侧(不妨设A,D),另外两个顶点在另一侧,则有a+b=c+d.
证明:如图所示,在①中有b-d=2OP,连接AC1,延长OP交AC1于R,

则PR为△AA1C1的中位线,故PR=
| AA1 |
| 2 |
| a |
| 2 |
| c |
| 2 |
| c |
| 2 |
| a |
| 2 |
所以,c-a=b-d,
即a+b=c+d.
③当直线只过某一顶点,(设过顶点A,点D在直线的一侧,B,C在直线的另一侧)则b=d+2c

④当直线与对角线重合时(不妨设是AC)则b=d.


练习册系列答案
相关题目