题目内容
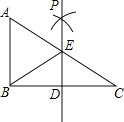
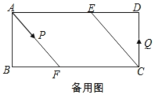
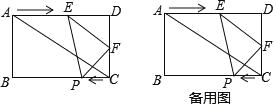
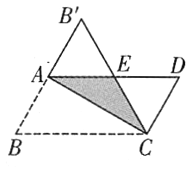
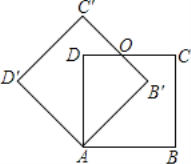
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转![]() 后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
【答案】![]() -1.
-1.
【解析】
根据题意可以推出△ADO≌△AB′O,所以重合部分的面积为2△ADO的面积,进而求出即可.
连接AO,连接B′C,
∵两个正方形的边长都为1,将其中一个固定不动,另一个绕顶点A旋转45°,
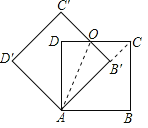
∴A,B′,C三点在一条直线上,
∴∠DAC=∠DCA=45°,
∴B′O=B′C,
在Rt△ADO和Rt△AB′O中,
![]() ,
,
∴Rt△ADO≌Rt△AB′O(HL),
∴OD=B′O,
设DO=x,
∴B′O=x,OC=1-x,
∴x2+x2=(1-x)2,
解得:x=-1-![]() (不合题意舍去),或x=-1+
(不合题意舍去),或x=-1+![]() ,
,
∴四边形AB′OD的面积=2S△AC′M=2×![]() ×1×(-1+
×1×(-1+![]() )=
)=![]() -1,
-1,
故答案为:![]() -1.
-1.

练习册系列答案
相关题目
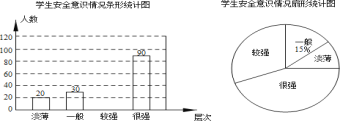
【题目】为了让同学们了解自己的体育水平,八年级1班的体育老师对全班50名学生进行了一次体育模拟测试(得分均为整数).成绩满分为10分,1班的体育委员根据这次测试成绩制作了如下的统计图:

(1)根据统计图所给的信息填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
男生 | 8 | ||
女生 | 8 | 8 |
(2)若女生队测试成绩的方差为1.76,请计算男生队测试成绩的方差.并说明在这次体育测试中,哪个队的测试成绩更整齐些?
【题目】某校举办的八年级学生数学素养大赛共设![]() 个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
七巧板拼图 | 趣题巧解 | 数学应用 | |
小米 |
|
|
|
小麦 |
|
|
|
![]() 若七巧板拼图,趣题巧解,数学应用三项得分分别
若七巧板拼图,趣题巧解,数学应用三项得分分别![]() 按折算计入总分,最终谁能获胜?
按折算计入总分,最终谁能获胜?
![]() 若七巧板拼图按
若七巧板拼图按![]() 折算,小麦 (填“可能”或“不可能”)获胜.
折算,小麦 (填“可能”或“不可能”)获胜.