题目内容
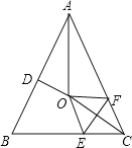
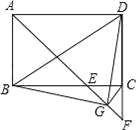
【题目】如图,在矩形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中正确的结论是______(填写所有正确结论的序号).
.其中正确的结论是______(填写所有正确结论的序号).
【答案】①③
【解析】
先求出∠BAE=45°,判断出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AB=BE,∠AEB=45°,从而得到BE=CD,故①正确;再求出△CEF是等腰直角三角形,根据等腰直角三角形的性质可得CG=EG,再求出∠BEG=∠DCG=135°,然后利用“边角边”证明△DCG≌△BEG,得到∠BGE=∠DGC,由∠BGE<∠AEB,得到∠DGC=∠BGE<45°,∠DGF<135°,故②错误;由∠CBG=∠CDG得到∠ABG+∠ADG=∠ABC+∠CBG+∠ADC-∠CDG=∠ABC+∠ADC=180°,故③正确.
在矩形![]() 中,
中,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,故①正确;
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
 ,
,
∴△DCG≌△BEG(SAS).
∴∠BGE=∠DGC,∠CBG=∠CDG
∵∠BGE<∠AEB,
∴∠DGC=∠BGE<45°,
∵∠CGF=90°,
∴∠DGF<135°,
故②错误;
∵∠CBG=∠CDG,
∴∠ABG+∠ADG=∠ABC+∠CBG+∠ADC-∠CDG=∠ABC+∠ADC=180°,
故③正确;
故答案为:①③.

【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆;
![]() 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆;
![]() 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?