Question

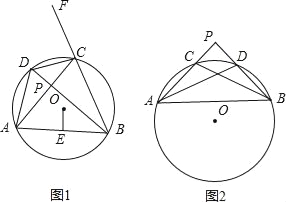
【题目】已知：如图1，四边形ABCD内接于⊙O，AC⊥BD于点P，OE⊥AB于点E，F为BC延长线上一点．

（1）求证：∠DCF=∠DAB；

（2）求证：；

（3）当图1中点P运动到圆外时，即AC、BD的延长线交于点P，且∠P=90°时（如图2所示），（2）中的结论是否成立？如果成立请给出你的证明，如果不成立请说明理由．

Answer 1

【答案】（1）详见解析；（2）；（3）见解析

【解析】

（1）利用三角形外角的性质可以得到∠DCF＝∠CBD＋∠CDB，再根据∠CBD＝∠DAC，∠CDB＝∠CAB即可得到结论；

（2）连接AO并延长交⊙O与点G，连接GB，利用三角形中位线的性质即可得到 ．

（3）结论仍然成立，证明方法同（2）．

（1）证明：∵∠DCF是△BDC的外角，

∴∠DCF=∠CBD+∠CDB．

∵∠CBD=∠DAC，∠CDB=∠CAB，

∴∠DCF=∠DAB．

（2）解：连接AO并延长交⊙O于点G，连接GB，

∵AG过O点，为圆O直径，

∴∠ABG=90°．

∵OE⊥AB于点E，

∴E为AB中点．

∴．

∵AC⊥BD，

∴∠APD=90°．

∴∠DAP+∠ADP=90°．

∵∠BAG+∠G=90°．且∠ADP=∠G，

∴∠DAP=∠BAG．

∴CD=BG．

∴．

（3）解：（2）的结论成立．

证明：连接AO并延长交⊙O于点G，连接GB，

∴∠ABG=90°．

∵OE⊥AB于点E，

∴E为AB中点．

∴．

由（2）证明可知，∠PDA=∠G，

∴∠PAD=∠BAG．

∴CD=BG．

∴．