Question

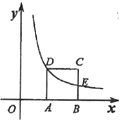
【题目】如图，边长为2的正方形的顶点在轴正半轴上，反比例函数的图像在第一象限的图像经过点，交于．

(1)当点的坐标为时，求和的值；

(2)若，求的面积．

Answer 1

【答案】（1）k=6；n=；（2）S△DOB=3．

【解析】

（1）由题意表示出点D的坐标，由反比例函数经过点D、E列出关于n的方程，求得n的值，进而求得k的值．

（2）设D（x，2），则E（x+2，），由反比例函数经过点D、E列出关于x的方程，求得x的值即可得出答案．

解：（1）∵正方形ABCD的边长为2，点E的坐标为（5，n），

∴OB=5，AB=AD=2，

∴D（3，2），

∵反比例函数y=在第一象限的图象经过点D，

∴k=3×2=6，

∴反比例为：y=，

∵反比例函数y=在第一象限的图象交BC于E，

∴n=；

（2）如图：连接OD、BD，

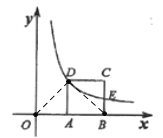
∵AB=AD=BC=2，

∴，

设D（x，2），则E（x+2，），

∵点D和点E在的图像上，

∴，

解得：，，

∴点D为（1，2），点B为（3，0），

∴OB=3，AD=2，

∴.