Question

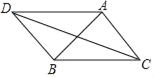
【题目】我们规定：等腰三角形的底角与顶角度数的比值叫做等腰三角形的“特征值”．如图，△ABC是以A为顶点的“特征值”为的等腰三角形，在△ABC外有一点D，若∠ADB＝∠ABC，AD＝4，BD＝3，则∠ABC＝_____度，CD的长是_____．

Answer 1

【答案】45

【解析】

设等腰三角形的底角为x，根据“特征值”的定义即可得：顶角为2x，再根据三角形的内角和定理即可求出x＝45°，即∠ABC＝45°，∠BAC＝90°，然后过C点作CH⊥DA垂足为H，交DB延长线于E，先证出△ADB∽△BEC，从而得出，根据等腰直角三角形的性质和已知条件即可求出BE＝4，CE＝3，从而求出EH的长，即可求出CH，然后根据勾股定理即可求出CD的长.

解：设等腰三角形的底角为x，

∵△ABC是以A为顶点的“特征值”为的等腰三角形，

根据定义可知顶角为2x．

∴x+x+2x＝180°，

∴x＝45°，

即∠ABC＝45°，∠BAC＝90°，

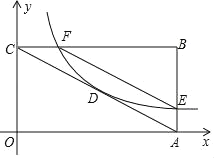
过C点作CH⊥DA垂足为H，交DB延长线于E，如图：

∵∠ADB+∠DAB＝∠ABC+∠CBE，∠ADB＝∠ABC＝45°，

∴∠ADB＝∠E＝45°，∠DAB＝∠EBC，

∴△ADB∽△BEC，

∴，

∵△ABC是等腰直角三角形，

∴，

∵AD＝4，BD＝3，

∴BE＝4，CE＝3，

∴DE＝3+4，

∵△DHE是等腰直角三角形，

∴DH＝EH＝＝，

∴CH＝EH－CE= ，

在Rt△DCH中，CD＝＝．

故答案为：45，．