Question

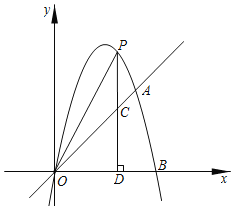
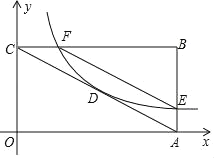
【题目】如图，在平面直角坐标系中，矩形OABC的两边分别在x轴、y轴上，D是对角线的交点，若反比例函数y＝的图象经过点D，且与矩形OABC的两边AB，BC分别交于点E，F．

（1）若D的坐标为（4，2）

①则OA的长是　 　，AB的长是　 　；

②请判断EF是否与AC平行，井说明理由；

③在x轴上是否存在一点P．使PD+PE的值最小，若存在，请求出点P的坐标及此时PD+PE的长；若不存在．请说明理由．

（2）若点D的坐标为（m，n），且m＞0，n＞0，求的值．

Answer 1

【答案】（1）①8；4；②EF∥AC，理由见解析；③当点P的坐标为（，0）时，PD+PE的值最小，最小值为5．

（2）＝．

【解析】

（1）①根据矩形的性质和点O、D的坐标即可求出点B的坐标，从而求出OA和AB的长；

②将点D坐标代入反比例函数解析式中即可求出反比例函数的解析式，从而求出E、F两点坐标，然后根据有两组对应边成比例且对应夹角相等的两个三角形相似，证出：△ABC∽△EBF，从而得出∠BCA＝∠BFE，根据平行线的判定即可证出EF∥AC；

③作点E关于x轴对称的点E′，连接DE′交x轴于点P，此时PD+PE的值最小，根据平面直角坐标系中任意两点之间的距离公式即可求出此时的DE′，然后利用待定系数法求出直线DE′的解析式，从而求出此时P点坐标；

（2）设点D的坐标为（m，n），与（1）①同理可得：点B的坐标为（2m，2n），然后与（1）②中同理可证：△ABC∽△EBF，从而求出.

解：（1）①∵四边形OABC是矩形，

∴D为OB的中点

∵点O的坐标为（0，0），点D的坐标为（4，2），

∴点B的坐标为（8，4），

∴OA＝8，AB＝4．

故答案为：8；4．

②EF∥AC，理由如下：

∵反比例函数y＝的图象经过点D（4，2），

∴k＝4×2＝8．

∵点B的坐标为（8，4），BC∥x轴，AB∥y轴，

∴点F的坐标为（2，4），点E的坐标为（8，1），

∴BF＝6，BE＝3，

∴＝，＝，

∴＝．

∵∠ABC＝∠EBF，

∴△ABC∽△EBF，

∴∠BCA＝∠BFE，

∴EF∥AC．

③作点E关于x轴对称的点E′，连接DE′交x轴于点P，根据两点之间，线段最短，此时PD+PE的值最小，并且PD+PE=PD+P E′= DE′，如图所示．

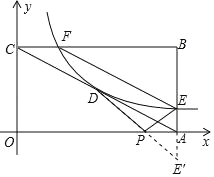
∵点E的坐标为（8，1），

∴点E′的坐标为（8，﹣1），

∴根据平面直角坐标系中任意两点之间的距离公式得：DE′＝＝5．

设直线DE′的解析式为y＝ax+b（a≠0），

将D（4，2），E′（8，﹣1）代入y＝ax+b，得：，

解得：，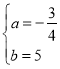

∴直线DE′的解析式为y＝﹣x+5．

当y＝0时，﹣x+5＝0，

解得：x＝，

∴当点P的坐标为（，0）时，PD+PE的值最小，最小值为5．

（2）∵点D的坐标为（m，n），

∴点B的坐标为（2m，2n）．

∵反比例函数y＝的图象经过点D（m，n），

∴k＝mn，

∴点F的坐标为（m，2n），点E的坐标为（2m，n），

∴BF＝m，BE＝n，

∴＝，＝，

∴＝．

又∵∠ABC＝∠EBF，

∴△ABC∽△EBF，

∴＝＝．