Question

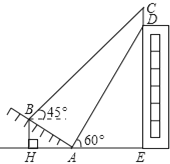
【题目】数轴上A、B、C三点分别对应实数a、1、c，且BC-AB=AC．下列选项中，满足A、B、C三点在数轴上的位置关系是（ 　）

A. B.

C. D.

Answer 1

【答案】A

【解析】分析：由BC-AB=AC，得到|c﹣1|﹣|a﹣1|=|a﹣c|，从选项数轴上找出a、b、c的关系，代入|c﹣1|﹣|a﹣1|=|a﹣c|，看是否成立．

详解：∵数轴上A、B、C三点所代表的数分别是a、1、c，设B表示的数为b，∴b=1．

∵BC-AB=AC，∴|c﹣1|﹣|a﹣1|=|a﹣c|，∴|c﹣b|﹣|a﹣b|=|a﹣c|．

A．b＜a＜c，则有|c﹣b|﹣|a﹣b|=c﹣b﹣a+b=c﹣a=|a﹣c|．正确；

B．c＜b＜a，则有|c﹣b|﹣|a﹣b|=b﹣c﹣a+b=2b﹣c﹣a≠|a﹣c|．故错误；

C．a＜c＜b，则有|c﹣b|﹣|a﹣b|=b﹣c﹣b+a=a﹣c≠|a﹣c|．故错误；

D．b＜c＜a，则有|c﹣b|﹣|a﹣b|=c﹣b﹣a+b=c﹣a≠|a﹣c|．故错误．

故选A．