题目内容
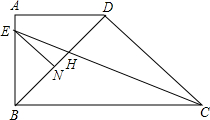
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(
+1)EH;③
=
.
其中正确的是( )
①BH=DH;②CH=(
| 2 |
| S△ENH |
| S△EBH |
| EH |
| EC |
其中正确的是( )
| A.①②③ | B.只有②③ | C.只有② | D.只有③ |

①如图,过H作HM⊥BC于M,
∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=
x=BE,
∴EN=x,
∴CD=BD=DH+BH=(
+1)x,
即
=
+1,
∵EN∥DC,
∴△DCH∽△NEH,
∴
=
=
+1,即CH=(
+1)EH;
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而
=
,
∴
=
.
所以正确的只有②③.
故选B.

∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=
| 2 |
∴EN=x,
∴CD=BD=DH+BH=(
| 2 |
即
| CD |
| EN |
| 2 |
∵EN∥DC,
∴△DCH∽△NEH,
∴
| CH |
| EH |
| CD |
| EN |
| 2 |
| 2 |
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而
| S△ENH |
| S△EBH |
| NH |
| BH |
∴
| S△ENH |
| S△EBH |
| EH |
| EC |
所以正确的只有②③.
故选B.


练习册系列答案
相关题目





