题目内容
【题目】如图，斜坡AB的坡度是i=1：2，坡角B处有一棵树BC，某一时刻测得树BC在斜坡AB上的影子BD的长度是10米，这时测得太阳光线与水平线的夹角为60°，则树BC的高度为多少米？（结果保留根号）．
【答案】解：过点D作DF⊥BG，垂足为F，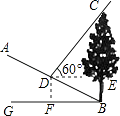
∵斜坡AB的坡度i=1：2，
∴设DF=x，BF=2x，则DB=10m，
∴x2+（2x）2=102 ，
解得：x=2 
，
故DE=4 ，BE=DF=2 ，
∵测得太阳光线与水平线的夹角为60°，
∴tan60°= 
= 
= 
，
解得：EC=4 
，
故BC=EC+BE=（2 +4 ）（m）．
【解析】根据题意首先利用勾股定理得出DF，DE的长，再利用锐角三角函数关系得出EC的长，进而得出答案．
【考点精析】关于本题考查的关于仰角俯角问题，需要了解仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能得出正确答案．
练习册系列答案
相关题目
