题目内容
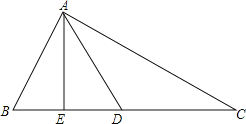
【题目】如图,在四边形ABCD中,AB∥CD,∠DAB=90°,且∠ABC=60°,AB=AC,△ADC的外接圆⊙O交BC于点E,连接DE并延长交AB延长线于点F.

(1)求证:CF=DB;
(2)当AD=![]() 时,求AB的长.
时,求AB的长.
【答案】详见解析.
【解析】
(1)连结AE,由∠ABC=60°,AB=BC可判断△ABC为等边三角形,由AB∥CD,∠DAB=90°得∠ADC=∠DAB=90°,则根据圆周角定理可得到AC为⊙O的直径,则∠AEC=90°,即AE⊥BC,根据等边三角形的性质得BE=CE,再证明△DCE≌△FBE,得到DE=FE,于是可判断四边形BDCF为平行四边形,根据平行四边形的性质得CF=DB;
(2)作EH⊥CF于H,由△ABC为等边三角形得∠BAC=60°,则∠DAC=30°,在Rt△ADC中,根据含30度的直角三角形三边的关系得DC=![]() AD=1,AC=2CD=2.
AD=1,AC=2CD=2.
则AB=AC=2
(1)证明:连结AE,如图,

∵∠ABC=60°,AB=BC,
∴△ABC为等边三角形,
∵AB∥CD,∠DAB=90°,![]()
∴∠ADC=∠DAB=90°,
∴AC为⊙O的直径,
∴∠AEC=90°,即AE⊥BC,
∴BE=CE,
CD∥BF,
∴∠DCE=∠FBE,
在△DCE和△FBE中,
 ,
,
∴△DCE≌△FBE(ASA),
∴DE=FE,
∴四边形BDCF为平行四边形,
∴CF=DB;
(2)解:作EH⊥CF于H,如图,
∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠DAC=30°,
在Rt△ADC中,AD=![]() ,
,
∴DC=![]() AD=1,AC=2CD=2,
AD=1,AC=2CD=2,
∴AB=AC=2.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目