题目内容
【题目】如图,已![]() 是
是![]() 的边
的边![]() 上的一点,
上的一点,![]() ,
,![]() =
=![]() ,
,![]() 是
是![]() 的中线.
的中线.
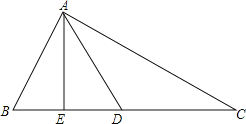
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求证:![]() 是
是![]() 的平分线.
的平分线.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据已知条件得到∠BAD=∠BDA=60°,于是得到AB=AD,等量代换得到CD=AD,根据等腰三角形的性质得到∠DAC=∠C,推出∠BDA=∠DAC+∠C=2∠C,即可得到结论;
(2)证明:延长AE到M,使EM=AE,连接DM,推出△ABE≌△MDE,根据全等三角形的性质得到∠B=∠MDE,AB=DM,根据全等三角形的判定定理得到△MAD≌△CAD,根据全等三角形的性质得到∠MAD=∠CAD,即可得到结论.
(1)解:∵∠B=60°,∠BDA=∠BAD,
∴∠BAD=∠BDA=60°,
∴AB=AD,
∵CD=AB,
∴CD=AD,
∴∠DAC=∠C,
∴∠BDA=∠DAC+∠C=2∠C,
∵∠BAD=60°,
∴∠C=30°;
(2)证明:延长AE到M,使EM=AE,连接DM,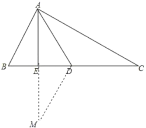
在△ABE和△MDE中,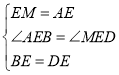 ,
,
∴△ABE≌△MDE,
∴∠B=∠MDE,AB=DM,
∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM,
在△MAD与△CAD,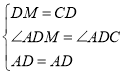 ,
,
∴△MAD≌△CAD,
∴∠MAD=∠CAD,
∴AD是∠EAC的平分线.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目