题目内容
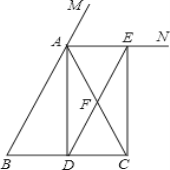
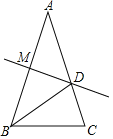
【题目】如图,已知AB=AC,∠A=36°,AB的垂直平分线MD交AC于点D,AB于M,以下结论:①△BCD是等腰三角形;②射线BD是△ACB的角平分线;③△BCD的周长C△BCD=AC+BC;④△ADM≌BCD.正确的有( )
A.①②③B.①②C.①③D.③④
【答案】C
【解析】
①由AB=AC,∠A=36°知∠ABC=∠C=72°,MN是AB的中垂线知AD=BD,∠ABD=∠A=36°,所以∠DBC=36°①正确;②由①和∠ABC=72°,可得∠ABD=36,②错误;③由①知,DA=BD,△BCD的周长=BC+CD+BD=AC+BC=AB+BC,③正确;④由①知∠AMD=90°,而△BCD为锐角三角形,所以④不正确.
由AB=AC,∠A=36°知∠ABC=∠C=72°,
∵MN是AB的中垂线,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠DBC=36°,
∴①正确,
又∵∠ABC=72°,
∴∠ABD=36°,
∴BD是△ACB的角平分线,
∵三角形的角平分线是线段,②错误,
由AD=BD,AB=AC知,△BCD的周长=BC+CD+BD=AC+BC=AB+BC,
∴③正确,
∵AM⊥MD,而△BCD为锐角三角形,
∴④错误,
∴正确的为:①③.
故选:C.

练习册系列答案
相关题目