Question

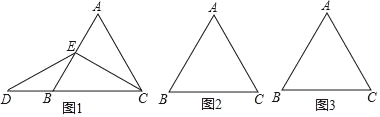
【题目】在等边三角形ABC中，E为直线AB上一点，连接EC．ED与直线BC交于点D，ED＝EC．

（1）如图1，AB＝1，点E是AB的中点，求BD的长；

（2）点E是AB边上任意一点（不与AB边的中点和端点重合），依题意，将图2补全，判断AE与BD间的数量关系并证明；

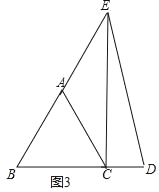
（3）点E不在线段AB上，请在图3中画出符合条件的一个图形．

Answer 1

【答案】（1）BD＝；（2）图2补全见解析，DB＝AE成立；理由见解析；（3）如图3所示．见解析.

【解析】

（1）根据等边三角形的性质得到∠BCE＝∠ACB＝30°，根据等腰三角形的性质得到∠D＝∠BCE＝30°，于是得到结论；

（2）过点E作EF∥BC，交AC于F，先证明△AEF是等边三角形，得出AE＝EF，再证明△DBE≌△EFC，得出DB＝EF，即可证出AE＝DB；

（3）根据题意作出图形即可．

（1）∵△ABC是等边三角形，点E是AB的中点，

∴∠BCE＝∠ACB＝30°，

∵ED＝EC，

∴∠D＝∠BCE＝30°，

∵∠ABC＝∠D+∠DEB＝60°，

∴∠DEB＝∠D＝30°，

∴BD＝BE＝AB＝；

（2）DB＝AE成立；理由如下：

如图2，过点E作EF∥BC，交AC于F，则∠AEF＝∠ABC，∠AFE＝∠ACB，∠CEF＝∠ECD，

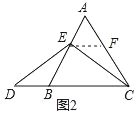
∵∠A＝∠ABC＝∠ACB＝60°，

∴∠A＝∠AEF＝∠AFE＝60°，

∠DBE＝120°，

∴△AEF是等边三角形，∴AE＝EF，∠EFC＝120°，

∴BE＝CF，∠DBE＝∠EFC，

∵ED＝EC，

∴∠D＝∠ECD，

∴∠D＝∠CEF，

在△DBE和△EFC中，

，

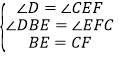∴△DBE≌△EFC（AAS），

∴DB＝EF，

∴AE＝DB；

（3）如图3所示．