题目内容
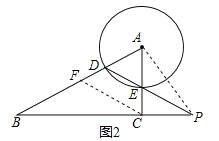
【题目】如图1,在Rt△ABC中,∠ACB = 90°.半径为1的⊙A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与边BC的延长线交于点P.
(1)当∠B = 30°时,求证:△ABC∽△EPC;
(2)当∠B = 30°时,连接AP,若△AEP与△BDP相似,求CE的长;
(3)若CE = 2,BD = BC,求∠BPD的正切值.

【答案】(1)答案见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由已知条件易求∠A=60°,又因为AD=AE,所以△ADE是等边三角形,进而可得∠CEP=60°,由三角形内角和定理可求∠P=30°,继而可证明△ABC∽△EPC;
(2)根据∠B=30°,∠ACB=90°可得∠BAC=60°,从而得到△ADE是等边三角形,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPD=30°,然后根据等角对等边的性质可得BD=PD,再根据△AEP与△BDP相似可得PE=AE,然后根据30°角所对的直角边等于斜边的一半即可求解;
(3)设BD=BC=x,表示出AB、AC的长度,然后利用勾股定理列式求出x的值为4,过点C作CF∥DP交AB于点F,再根据平行线分线段成比例定理求出DF=2,然后求出BF的长度,再次利用平行线分线段成比例定理求出CP的长度,然后根据正切的定义解答即可.
试题解析:解:(1)∵∠ACB=90°,∠B=30°,∴∠A=60°,∵AD=AE,∴△ADE是等边三角形,∴∠ADE=∠AED=60°,∴∠PEC=∠AED=60°,∵∠ACB=∠ECP=90°,∴∠P=30°,∴△ABC∽△EPC;
(2)∵∠B=30°,∠ACB=90°,∴∠BAC=90°﹣30°=60°,∴△ADE是等边三角形,在△BDP中,∠ADE=∠B+∠BPD,即60°=30°+∠BPD,解得∠BPD=30°,∴∠B=∠BPD,∴BD=PD,∵△AEP与△BDP相似,∴AE=PE,∵⊙A的半径为1,∴PE=1,在Rt△PCE中,CE=![]() PE=
PE=![]() ;
;
(3)设BD=BC=x,∵⊙A的半径为1,CE=2,∴AB=x+1,AC=2+1=3,∵∠ACB=90°,∴AC2+BC2=AB2,即32+x2=(x+1)2,解得x=4,过点C作CF∥DP交AB于点F,(如图2)
则![]() ,
,![]() ,即
,即![]() =
=![]() ,解得DF=2,∴BF=BD﹣DF=4﹣2=2,又由CF∥DP可得
,解得DF=2,∴BF=BD﹣DF=4﹣2=2,又由CF∥DP可得![]() ,即
,即![]() ,解得CP=4,∴tan∠BPD=
,解得CP=4,∴tan∠BPD=![]() =
=![]() =
=![]() .
.