题目内容
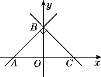
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.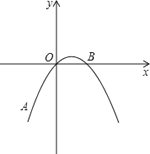
【答案】解:(1)把A(﹣2,﹣4),O(0,0),B(2,0)三点的坐标代入y=ax2+bx+c中,得
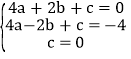 ,解这个方程组,得
,解这个方程组,得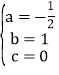 。
。
∴抛物线的解析式为y=﹣![]() x2+x。
x2+x。
(2)由y=﹣![]() x2+x=﹣
x2+x=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,可得
,可得
抛物线的对称轴为x=1,并且对称轴垂直平分线段OB。
∴OM=BM。∴OM+AM=BM+AM。
连接AB交直线x=1于M点,则此时OM+AM最小。
过点A作AN⊥x轴于点N,
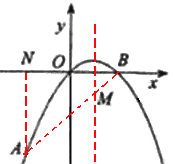
在Rt△ABN中,![]() ,
,
因此OM+AM最小值为![]() 。
。
【解析】
二次函数综合题,曲线上点的坐标与方程的关系,解方程组,二次函数的性质,线段中垂线的性质,三角形三边关系,勾股定理。
(2)根据O、B点的坐标发现:抛物线上,O、B两点正好关于抛物线的对称轴对称,那么只需连接A、B,直线AB和抛物线对称轴的交点即为符合要求的M点,而AM+OM的最小值正好是AB的长。
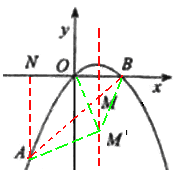
对x=1上其它任一点M′,根据三角形两边之和大于第三边的性质,总有:
O M′+A M′=" B" M′+A M′>AB=OM+AM,
即OM+AM为最小值。

练习册系列答案
相关题目