Question

【题目】如图1，在平面直角坐标系xOy中，A（0，4），B（8，0），C（8，4）.

⑴ 试说明四边形AOBC是矩形.

⑵ 在x轴上取一点D，将△DCB绕点C逆时针旋转90°得到（点与点D对应）.

① 若OD＝3，求点的坐标.

② 连接AD'、OD'，则AD'＋OD'是否存在最小值，若存在，请直接写出最小值及此时点D'的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）证明见解析；（2）①D'（12，－1）或D'（12，－7）②最小值为或4，此时点D'（12，2）

【解析】分析： 根据有一个角是直角的平行四边形即可判定.

①分当点D在原点右侧时和当点D在原点左侧时两种情况进行讨论.

②画出图形，解答即可.

详解：⑴ ∵ A（0，4），B（8，0），C（8，4）,

∴ OA=4，BC=4，OB=8，AC=8,

∴ OA=BC，AC=OB,

∴ 四边形AOBC是平行四边形 ,

∵ ∠AOB=90°,

∴ □AOBC是矩形,

⑵ ∵ □AOBC是矩形,

∴ ∠ACB=90°，∠OBC=90°,

∵将△DCB绕点C逆时针旋转90°得到（点与点D对应）,

∴， ， ,

，

∴⊥AC,

如图，当点D在原点右侧时： ,

∴ 点的坐标为

如图，当点D在原点左侧时： ,

∴ 点的坐标为

综上所述：点的坐标为或

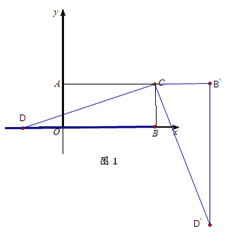
②如图所示：

AD'＋OD'的最小值是最小值为或4，此时点D'