题目内容
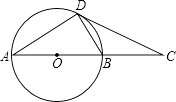
【题目】如图，在△ABC中，D是边AC上一点，连BD，给出下列条件：①∠ABD=∠ACB；②AB2=ADAC；③ADBC=ABBD；④ABBC=ACBD．其中单独能够判定△ABC∽△ADB的个数是（ ） 
A.①②
B.①②③
C.①②④
D.①②③④
【答案】A
【解析】解：①∵∠ABD=∠ACB，∠A=∠A，∴△ABC∽△ADB； ②∵AB2=ADAC，∴ 
，∠A=∠A，△ABC∽△ADB；
③∵ADBC=ABBD，∴ 
= 
，∠A=∠A，△ABC与△ADB不相似；
④∵ABBC=ACBD，∴ 
= ，∠A=∠A，△ABC与△ADB不相似；
故选：A．
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识，掌握相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．
练习册系列答案
智慧小复习系列答案
相关题目
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：
碟子的个数 | 碟子的高度（单位：cm） |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |
（1）当桌子上放有x（个）碟子时，请写出此时碟子的高度（用含x的式子表示）；
（2）分别从三个方向上看，其三视图如上图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．
