题目内容
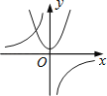
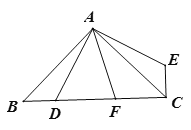
【题目】如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.
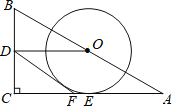
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)当∠A=30°,CF![]() 时,求⊙O的半径.
时,求⊙O的半径.
【答案】(1)结论:DF是⊙O的切线.理由见解析;(2)OE=1.
【解析】
(1)结论:DF是⊙O的切线.作OG⊥DF于G.连接OE.想办法证明OG=OE即可解决问题;
(2)由FA,FD是⊙O的切线,推出FG=FE,设FG=FE=x,由△OGD≌△DCF(AAS),推出DG=CF=![]() ,推出OD=DF=
,推出OD=DF=![]() +x,由AC=2OD,CE=OD,推出AE=EC=OD=
+x,由AC=2OD,CE=OD,推出AE=EC=OD=![]() +x,由∠A=30°,推出CD=OE=
+x,由∠A=30°,推出CD=OE=![]() ,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题;
,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题;
(1)结论:DF是⊙O的切线.
理由:作OG⊥DF于G.连接OE.
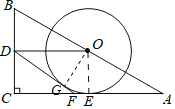
∵BD=DC,BO=OA,
∴OD∥AC,
∴∠ODG=∠DFC,
∵∠OGD=∠DCF=90°,OD=DF,
∴△OGD≌△DCF(AAS),
∴OG=CD,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠AEO=∠C=90°,
∴OE∥BC,
∵OD∥CD,
∴四边形CDOE是平行四边形,
∴CD=OE,
∴OG=OE,
∴DF是⊙O的切线.
(2)∵FA,FD是⊙O的切线,
∴FG=FE,设FG=FE=x,
∵△OGD≌△DCF(AAS),
∴DG=CF=![]() ,
,
∴OD=DF=![]() +x,
+x,
∵AC=2OD,CE=OD,
∴AE=EC=OD=![]() +x,
+x,
∵∠A=30°,
∴CD=OE=![]() ,
,
在Rt△DCF中,∵DF2=CD2+CF2,
∴(![]() +x)2=(
+x)2=(![]() )2+(
)2+(![]() )2,
)2,
解得x=![]() -
-![]() 或-
或-![]() -
-![]() (舍弃),
(舍弃),
∴OE=![]() =1.
=1.

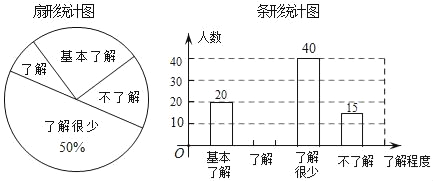
【题目】某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
成绩 | 人数(频数) | 百分比(频率) |
0 | ||
5 | 0.2 | |
10 | 5 | |
15 | 0.4 | |
20 | 5 | 0.1 |
根据表中已有的信息,下列结论正确的是( )
A. 共有40名同学参加知识竞赛
B. 抽到的同学参加知识竞赛的平均成绩为10分
C. 已知该校共有800名学生,若都参加竞赛,得0分的估计有100人
D. 抽到同学参加知识竞赛成绩的中位数为15分