题目内容
抛物线 交
交 轴于
轴于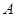 、
、 两点,交
两点,交 轴于点
轴于点 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
,
(1)求二次函数 的解析式;
的解析式;
在抛物线对称轴上是否存在一点 ,使点
,使点 到
到 、
、 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与 轴相切,求此圆的半径.
轴相切,求此圆的半径.
 交
交 轴于
轴于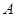 、
、 两点,交
两点,交 轴于点
轴于点 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
,(1)求二次函数
 的解析式;
的解析式;在抛物线对称轴上是否存在一点
 ,使点
,使点 到
到 、
、 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;平行于
 轴的一条直线交抛物线于
轴的一条直线交抛物线于 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与 轴相切,求此圆的半径.
轴相切,求此圆的半径.
(1)将 代入
代入 ,
,
得 .
.
将 ,
, 代入
代入 ,
,
得 .……….(1)
.……….(1)
∵ 是对称轴,
是对称轴,
∴ . (2)
. (2)
将(2)代入(1)得
 ,
,  .
.
所以,二次函数得解析式是 .
.
(2) 与对称轴的交点
与对称轴的交点 即为到
即为到 的距离之差最大的点.
的距离之差最大的点.
∵ 点的坐标为
点的坐标为 ,
,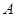 点的坐标为
点的坐标为 ,
,
∴ 直线 的解析式是
的解析式是 ,
,
又对称轴为 ,
,
∴ 点 的坐标
的坐标 .
.
(3)设 、
、 ,所求圆的半径为r,
,所求圆的半径为r,
则 ,……………(1)
,……………(1)
∵ 对称轴为 ,
,
∴ . ……………(2)
. ……………(2)
由(1)、(2)得: .………(3)
.………(3)
将 代入解析式
代入解析式 ,
,
得 ,…………(4)
,…………(4)
整理得: .
.
由于 r=±y,当 时,
时, ,
,
解得, ,
,  (舍去),
(舍去),
当 时,
时, ,
,
解得, ,
,  (舍去).
(舍去).
所以圆的半径是 或
或 .
.
 代入
代入 ,
,得
 .
.将
 ,
, 代入
代入 ,
,得
 .……….(1)
.……….(1)∵
 是对称轴,
是对称轴,∴
 . (2)
. (2) 将(2)代入(1)得
 ,
,  .
.所以,二次函数得解析式是
 .
.(2)
 与对称轴的交点
与对称轴的交点 即为到
即为到 的距离之差最大的点.
的距离之差最大的点.∵
 点的坐标为
点的坐标为 ,
,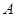 点的坐标为
点的坐标为 ,
,∴ 直线
 的解析式是
的解析式是 ,
,又对称轴为
 ,
,∴ 点
 的坐标
的坐标 .
. (3)设
 、
、 ,所求圆的半径为r,
,所求圆的半径为r,则
 ,……………(1)
,……………(1)∵ 对称轴为
 ,
,∴
 . ……………(2)
. ……………(2)由(1)、(2)得:
 .………(3)
.………(3) 将
 代入解析式
代入解析式 ,
,得
 ,…………(4)
,…………(4)整理得:
 .
.由于 r=±y,当
 时,
时, ,
,解得,
 ,
,  (舍去),
(舍去),当
 时,
时, ,
,解得,
 ,
,  (舍去).
(舍去).所以圆的半径是
 或
或 .
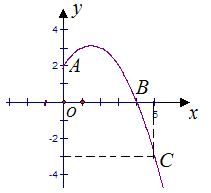
.(1)根据抛物线过C点,可得出c=-3,对称轴x=1,则- =1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.
=1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.
(2)本题的关键是要确定P点的位置,由于A、B关于抛物线的对称轴对称,因此可连接AC,那么P点就是直线AC与对称轴的交点.可根据A、C的坐标求出AC所在直线的解析式,进而可根据抛物线对称轴的解析式求出P点的坐标.
(3)根据圆和抛物线的对称性可知:圆心必在对称轴上.因此可用半径r表示出M、N的坐标,然后代入抛物线中即可求出r的值.
 =1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.
=1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.(2)本题的关键是要确定P点的位置,由于A、B关于抛物线的对称轴对称,因此可连接AC,那么P点就是直线AC与对称轴的交点.可根据A、C的坐标求出AC所在直线的解析式,进而可根据抛物线对称轴的解析式求出P点的坐标.
(3)根据圆和抛物线的对称性可知:圆心必在对称轴上.因此可用半径r表示出M、N的坐标,然后代入抛物线中即可求出r的值.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 ,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
 ,对称轴
,对称轴 ,抛物线与
,抛物线与 轴两交点距离为4,求这个二次函数的解析式?
轴两交点距离为4,求这个二次函数的解析式? 中,
中, ,
, .它的顶点
.它的顶点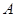 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,
, ,点
,点 从点
从点 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点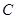 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
 的度数.
的度数. 上运动时,
上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点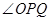 的大小随着时间
的大小随着时间 边运动时,
边运动时, 的点
的点
 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值. 的图像过第一、三、四象限,则函数
的图像过第一、三、四象限,则函数 ( )
( )

