题目内容
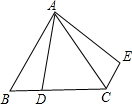（2012•广州）如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为2
2
．分析：由在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，根据等边三角形的性质，即可求得BD的长，然后由旋转的性质，即可求得CE的长度．
解答：解：∵在等边三角形ABC中，AB=6，
∴BC=AB=6，
∵BC=3BD，
∴BD=
BC=2，
∵△ABD绕点A旋转后得到△ACE，
∴△ABD≌△ACE，
∴CE=BD=2．
故答案为：2．
∴BC=AB=6，
∵BC=3BD，
∴BD=
| 1 |
| 3 |
∵△ABD绕点A旋转后得到△ACE，
∴△ABD≌△ACE，
∴CE=BD=2．
故答案为：2．
点评：此题考查了旋转的性质与等边三角形的性质．此题难度不大，注意旋转中的对应关系．
练习册系列答案
阅读快车系列答案
相关题目
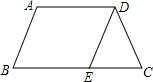（2012•广州）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是（ ）
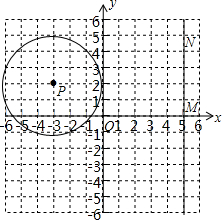（2012•广州）如图，⊙P的圆心为P（-3，2），半径为3，直线MN过点M（5，0）且平行于y轴，点N在点M的上方．
（2012•广州）如图，抛物线y=
（2012•广州）如图，在平行四边形ABCD中，AB=5，BC=10，F为AD的中点，CE⊥AB于E，设∠ABC=α（60°≤α＜90°）．