题目内容
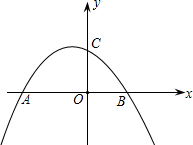 (2012•广州)如图,抛物线y=-
(2012•广州)如图,抛物线y=-| 3 |
| 8 |
| 3 |
| 4 |
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
分析:(1)A、B点为抛物线与x轴交点,令y=0,解一元二次方程即可.
(2)根据题意求出△ACD中AC边上的高,设为h.在坐标平面内,作AC的平行线,平行线之间的距离等于h.根据等底等高面积相等,可知平行线与坐标轴的交点即为所求的D点.
从一次函数的观点来看,这样的平行线可以看做是直线AC向上或向下平移而形成.因此先求出直线AC的解析式,再求出平移距离,即可求得所作平行线的解析式,从而求得D点坐标.
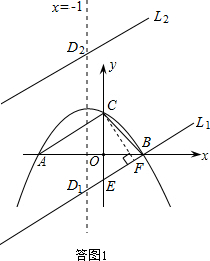
注意:这样的平行线有两条,如答图1所示.
(3)本问关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义.
因为过A、B点作x轴的垂线,其与直线l的两个交点均可以与A、B点构成直角三角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置关系方面考虑,以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点与A、B点构成直角三角形.从而问题得解.
注意:这样的切线有两条,如答图2所示.
(2)根据题意求出△ACD中AC边上的高,设为h.在坐标平面内,作AC的平行线,平行线之间的距离等于h.根据等底等高面积相等,可知平行线与坐标轴的交点即为所求的D点.
从一次函数的观点来看,这样的平行线可以看做是直线AC向上或向下平移而形成.因此先求出直线AC的解析式,再求出平移距离,即可求得所作平行线的解析式,从而求得D点坐标.
注意:这样的平行线有两条,如答图1所示.
(3)本问关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义.
因为过A、B点作x轴的垂线,其与直线l的两个交点均可以与A、B点构成直角三角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置关系方面考虑,以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点与A、B点构成直角三角形.从而问题得解.
注意:这样的切线有两条,如答图2所示.
解答:解:(1)令y=0,即-
x2-
x+3=0,
解得x1=-4,x2=2,
∴A、B点的坐标为A(-4,0)、B(2,0).
(2)抛物线y=-
x2-
x+3的对称轴是直线x=-
=-1,
即D点的横坐标是-1,
 S△ACB=
S△ACB=
AB•OC=9,
在Rt△AOC中,AC=
=
=5,
设△ACD中AC边上的高为h,则有
AC•h=9,解得h=
.
如答图1,在坐标平面内作直线平行于AC,且到AC的距离=h=
,这样的直线有2条,分别是l1和l2,则直线与对称轴x=-1的两个交点即为所求的点D.
设l1交y轴于E,过C作CF⊥l1于F,则CF=h=
,
∴CE=
=
=
=
.
设直线AC的解析式为y=kx+b,将A(-4,0),C(0,3)坐标代入,
得到
,解得
,
∴直线AC解析式为y=
x+3.
直线l1可以看做直线AC向下平移CE长度单位(
个长度单位)而形成的,
∴直线l1的解析式为y=
x+3-
=
x-
.
则D1的纵坐标为
×(-1)-
=-
,∴D1(-1,-
).
同理,直线AC向上平移
个长度单位得到l2,可求得D2(-1,
)
综上所述,D点坐标为:D1(-1,-
),D2(-1,
).
(3)如答图2,以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N.
∵A(-4,0),B(2,0),
∴F(-1,0),⊙F半径FM=FB=3.
又FE=5,则在Rt△MEF中,
ME=
=4,sin∠MFE=
,cos∠MFE=
.
在Rt△FMN中,MN=MF•sin∠MFE=3×
=
,
FN=MF•cos∠MFE=3×
=
,则ON=
,
∴M点坐标为(
,
)
直线l过M(
,
),E(4,0),
设直线l的解析式为y=kx+b,则有
,解得
,
所以直线l的解析式为y=-
x+3.
同理,可以求得另一条切线的解析式为y=
x-3.
综上所述,直线l的解析式为y=-
x+3或y=
x-3.
| 3 |
| 8 |
| 3 |
| 4 |
解得x1=-4,x2=2,
∴A、B点的坐标为A(-4,0)、B(2,0).
(2)抛物线y=-
| 3 |
| 8 |
| 3 |
| 4 |
-
| ||
2×(-
|
即D点的横坐标是-1,
 S△ACB=
S△ACB=| 1 |
| 2 |
在Rt△AOC中,AC=
| OA2+OC2 |
| 42+32 |
设△ACD中AC边上的高为h,则有
| 1 |
| 2 |
| 18 |
| 5 |
如答图1,在坐标平面内作直线平行于AC,且到AC的距离=h=
| 18 |
| 5 |
设l1交y轴于E,过C作CF⊥l1于F,则CF=h=
| 18 |
| 5 |
∴CE=
| CF |
| sin∠CEF |
| CF |
| sin∠OCA |
| ||
|
| 9 |
| 2 |
设直线AC的解析式为y=kx+b,将A(-4,0),C(0,3)坐标代入,
得到
|
|
∴直线AC解析式为y=
| 3 |
| 4 |
直线l1可以看做直线AC向下平移CE长度单位(
| 9 |
| 2 |
∴直线l1的解析式为y=
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
则D1的纵坐标为
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
同理,直线AC向上平移
| 9 |
| 2 |
| 27 |
| 4 |
综上所述,D点坐标为:D1(-1,-
| 9 |
| 4 |
| 27 |
| 4 |
(3)如答图2,以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N.

∵A(-4,0),B(2,0),
∴F(-1,0),⊙F半径FM=FB=3.
又FE=5,则在Rt△MEF中,
ME=
| 52-32 |
| 4 |
| 5 |
| 3 |
| 5 |
在Rt△FMN中,MN=MF•sin∠MFE=3×
| 4 |
| 5 |
| 12 |
| 5 |
FN=MF•cos∠MFE=3×
| 3 |
| 5 |
| 9 |
| 5 |
| 4 |
| 5 |
∴M点坐标为(
| 4 |
| 5 |
| 12 |
| 5 |
直线l过M(
| 4 |
| 5 |
| 12 |
| 5 |
设直线l的解析式为y=kx+b,则有
|
|
所以直线l的解析式为y=-
| 3 |
| 4 |
同理,可以求得另一条切线的解析式为y=
| 3 |
| 4 |
综上所述,直线l的解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题解题关键是二次函数、一次函数以及圆等知识的综合运用.难点在于第(3)问中对于“以A、B、M为顶点所作的直角三角形有且只有三个”条件的理解,这可以从直线与圆的位置关系方面入手解决.本题难度较大,需要同学们对所学知识融会贯通、灵活运用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
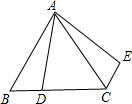 (2012•广州)如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为
(2012•广州)如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )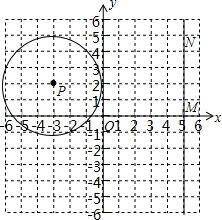 (2012•广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(2012•广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.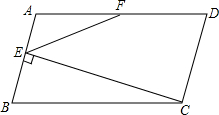 (2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).