Question

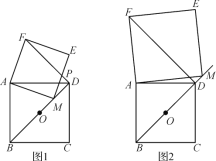
【题目】已知O为正方形ABCD的中心，M为射线OD上一动点(M与点O，D不重合)，以线段AM为一边作正方形AMEF，连接FD.

(1)当点M在线段OD上时(如图1)，线段BM与DF有怎样的数量及位置关系？请说明理由；

(2)当点M在线段OD的延长线上时(如图2)，(1)中的结论是否仍然成立？请结合图2说明理由.

Answer 1

【答案】(1)BM＝DF，BM⊥DF.理由见解析；(2)BM＝DF，BM⊥DF仍然成立，理由见解析.

【解析】

（1）根据图形，由正方形的性质证得△FAD≌△MAB，进而求出BM＝DF，∠FDA＝∠ABD＝45°，结合已知条件即可推出BM=DF，BM⊥DF；
（2）成立，根据正方形的性质，推出△ABM≌△ADF，根据正方形的性质推出∠BAM=∠DAF，△ABM≌△ADF，进而求出BM=DF，∠ABM=∠ADF，∠BDF=∠ADB+∠ADF=90°即可.

(1)BM＝DF，BM⊥DF.

理由：∵四边形ABCD，AMEF均为正方形，

∴AF＝AM，AD＝AB，∠FAM＝∠DAB＝90°，

∴∠FAM－∠DAM＝∠DAB－∠DAM，即∠FAD＝∠MAB.

在△FAD和△MAB中，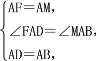

∴△FAD≌△MAB(SAS)，∴BM＝DF，∠FDA＝∠ABD＝45°.

∵∠ADB＝45°，∴∠FDB＝45°＋45°＝90°.∴BM⊥DF，即BM＝DF，BM⊥DF.

(2)BM＝DF，BM⊥DF仍然成立，

理由：∵四边形ABCD和AMEF均为正方形，∴AB＝AD，AM＝AF，∠BAD＝∠MAF＝90°，

∴∠FAM＋∠DAM＝∠DAB＋∠DAM，即∠FAD＝∠MAB.

在△FAD和△MAB中，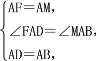

∴△FAD≌△MAB(SAS)，∴BM＝DF，∠ABM＝∠ADF.

由正方形ABCD知，∠ABM＝∠ADB＝45°，

∴∠BDF＝∠ADB＋∠ADF＝90°，即BM⊥DF.

∴(1)中的结论仍成立.