题目内容
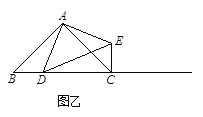
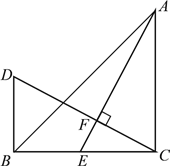
【题目】如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D;若AC=12cm,求BD的长;
【答案】6.
【解析】试题分析:首先根据DB⊥BC,CF⊥AE得出∠D=∠AEC,从而得出△DBC≌△ECA,根据全等得出BC=AC=12cm,BD=CE,最后根据中点的性质得出答案.
试题解析:∵DB⊥BC,CF⊥AE,∴∠DCB+∠D=∠DCB+∠AEC=90°,∴∠D=∠AEC,
又∵∠DBC=∠ECA=90°,且BC=CA, ∴△DBC≌△ECA(AAS),
∴BC=AC=12cm,BD=CE,又∵E为BC的中点,∴BD=CE=![]() BC=6cm.
BC=6cm.

练习册系列答案
相关题目