题目内容
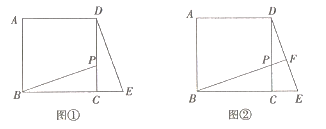
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
【答案】探究:90;应用:![]() ;拓展:42
;拓展:42
【解析】
(1)由旋转性质即可得到旋转角的度数;
(2)由旋转的性质,得到![]() ≌
≌![]() ,由全等三角形对应角相等,得到
,由全等三角形对应角相等,得到![]() ,再由直角三角形两个锐角互余和等量代换,即可得到
,再由直角三角形两个锐角互余和等量代换,即可得到![]() ,即
,即![]() ;
;
(3)由![]() ≌
≌![]() ,得到CE=PC,由DP=2CP,BC=6,得CE=2,则四边形ABED的面积=S正方形ABCD+S△CDE.
,得到CE=PC,由DP=2CP,BC=6,得CE=2,则四边形ABED的面积=S正方形ABCD+S△CDE.
探究:由旋转性质可得旋转角=∠BCD=∠DCE=90°;
故答案为:90°;
应用:由旋转,得![]() ≌
≌![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
拓展:∵![]() ≌
≌![]() ,
,
∴CE=PC,
∵DP=2CP,BC=6,
∴CE=2,
∴S四边形ABED =S正方形ABCD+S△CDE=6×6+![]() ×6×2=36+6=42,
×6×2=36+6=42,
故答案为:42.

练习册系列答案
相关题目