题目内容
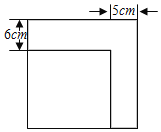
【题目】如图,在平面直角坐标系中,点D是正方形OABC的边AB上的动点,OC=6.以AD为一边在AB的右侧作正方形ADEF,连结BF交DE于P点.
(1)请直接写出点A、B的坐标;
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系?若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
(3)当P点为线段DE的三等分点时,试求出AF的长度.

【答案】(1)A(6,0),B(6,6);(2)OD⊥BF,理由见解析;(3)当P点为线段DE的三等分点时,AF的长度为2或4.
【解析】
(1)利用正方形的性质得出OA=AB=6,即可得出结论;
(2)利用SAS判断出△AOD≌△BAF,进而得出∠AOD=∠BAF,即可得出结论;
(3)先表示出BD,DP,再判断出△BDP∽△BAF,得出![]() ,代入解方程即可得出结论。
,代入解方程即可得出结论。
(1)∵四边形OABC是正方形,
∴BC⊥OC,AB⊥OA,OB=AB=BC=OC,
∵OC=6,
∴BC=AB=6,
∴A(6,0),B(6,6);

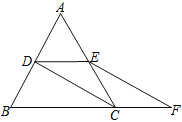
(2)OD⊥BF,理由:如图,延长OD交BF于G,
∵四边形ADEF是正方形,
∴AD=AF,∠BAF=∠OAD,
在△AOD和△BAF中, ,
,
∴△AOD≌△BAF(SAS),
∴∠AOD=∠BAF,
∴∠BAF+∠AFB=90°,
∴∠AOD+AFB=90°,
∴∠OGF=90°,
∴OD⊥BF;
(3)设正方形ADEF的边长为x,
∴AF=AD=DE=x,
∴BD=AB﹣AD=6﹣x,
∵点P是DE的三等分点,
∴DP=![]() AF=
AF=![]() x或DP=
x或DP=![]() AF=
AF=![]() x
x
∵DE∥AF,
∴△BDP∽△BAF,
∴![]() ,
,
∴ 或
或![]() ,
,
∴x=4或x=2,
当P点为线段DE的三等分点时,AF的长度为2或4.

练习册系列答案
相关题目