��Ŀ����
����Ŀ����֪����������A��B����ʾ�����ֱ�Ϊa��b��������|a��3|��(b��9)2��0��OΪԭ�㣻

(1) a�� ��b�� .
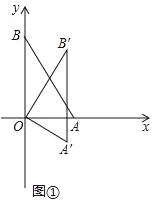
(2) ����C��O����������˶�������3����C��A��ľ�����ڵ�C��B����룬���C���˶��ٶȣ���������ᣬ���з���.��
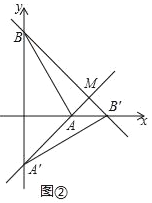
(3) ����D��2����λÿ����ٶȴӵ�O�����˶���ͬʱ��P�ӵ�A������3����λÿ����ٶ������˶�����Q�ӵ�B��������6����λÿ����ٶ������˶������˶������У�M��N�ֱ�ΪPD��OQ���е㣬��![]() ��ֵ�Ƿ����仯����˵������.��ע��PDָ���ǵ�P��D֮����߶Σ�����ʽPQ��ODָ�߶�PQ��OD���ȵIJ�.���Ƶģ�������������д��ĸд��һ��ʱ����һ����.
��ֵ�Ƿ����仯����˵������.��ע��PDָ���ǵ�P��D֮����߶Σ�����ʽPQ��ODָ�߶�PQ��OD���ȵIJ�.���Ƶģ�������������д��ĸд��һ��ʱ����һ����.
���𰸡���1��-3��9����2����C���ٶ�Ϊÿ��1����λ���ȣ���3��![]() ��ֵû�з����仯�����ɼ�����.
��ֵû�з����仯�����ɼ�����.
��������
��1�����ݼ����Ǹ����ĺ�Ϊ0����ÿһ��������0����������a��b�ķ��̼������a��b��ֵ����2�����ݵ�C��O����������˶�������3����C��A��ľ�����ڵ�C��B����룬�ɱ�ʾ![]() ��
��![]() ������CA=CB��������x�ķ�����⼴�ɣ���3�����ݵ���˶��ٶȺͷ��ֱ��ú�t�Ĵ���ʽ��ʾ��D��P��Q��M��N��Ӧ�������ٷֱ����PQ��OD��MN�ij���Ȼ�����
������CA=CB��������x�ķ�����⼴�ɣ���3�����ݵ���˶��ٶȺͷ��ֱ��ú�t�Ĵ���ʽ��ʾ��D��P��Q��M��N��Ӧ�������ٷֱ����PQ��OD��MN�ij���Ȼ�����![]() ��ֵΪ���������ɵó�����.
��ֵΪ���������ɵó�����.
��1����|a��3|��(b��9)2��0��
��a+3=0��b-9=0�����a=-3��b=9��
��2����3����C��Ӧ����Ϊx��
��![]() ��
��![]() ��
��
��CA=CB����![]() ��
��
��![]() ���⣻
���⣻
��![]() �����x=3����ʱ��C���ٶ�Ϊ3��3=1����λÿ�룬
�����x=3����ʱ��C���ٶ�Ϊ3��3=1����λÿ�룬
���C���ٶ�Ϊÿ��1����λ���ȣ�
��3��![]() ��ֵû�з����仯���������£����˶�ʱ��Ϊt�룬
��ֵû�з����仯���������£����˶�ʱ��Ϊt�룬
���D��Ӧ����Ϊ2t��
��P��Ӧ����Ϊ-3-3t��
��Q��Ӧ����Ϊ9+6t��
��M��Ӧ����Ϊ-1.5-0.5t��
��N��Ӧ����Ϊ4.5+3t��
��PQ=9t+12��OD=2t��MN=3.5t+6��
��![]() ��Ϊ��ֵ��
��Ϊ��ֵ��
��![]() ��ֵû�з����仯.
��ֵû�з����仯.

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д�����Ŀ��Ϊ�˱���������ij�������ۺ�����ָ�Ӳ���������A��B�����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����A�ͺŵ���ˮ�����豸��̨������75��Ԫ����B�ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
��ˮ�����豸 | A�� | B�� |
�۸���Ԫ/̨�� | m | m-3 |
�´�����ˮ������/̨�� | 220 | 180 |
��1����m��ֵ��
��2���������ʽ����ƣ�ָ�Ӳ����ڹ�����ˮ�����豸���ʽ���165��Ԫ�����ж����ֹ����������ÿ����ദ����ˮ���Ķ�����