Question

【题目】如图1，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点C，抛物线经过A、C两点，与x轴的另一交点为点B．

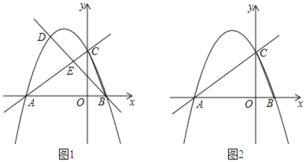
（1）求抛物线的函数表达式；（2）点D为直线AC上方抛物线上一动点，

①连接BC、CD、BD，设BD交直线AC于点E，△CDE的面积为S1，△BCE的面积为S2．求：的最大值；

②如图2，是否存在点D，使得∠DCA＝2∠BAC？若存在，直接写出点D的坐标，若不存在，说明理由．

Answer 1

【答案】（1）；（2）①当时，的最大值是；②点D的坐标是

【解析】

（1）根据题意得到A（-4，0），C（0，2）代入y=-x2+bx+c，于是得到结论；

（2）①如图，令y=0，解方程得到x1=-4，x2=1，求得B（1，0），过D作DM⊥x轴于M，过B作BN⊥x轴交于AC于N，根据相似三角形的性质即可得到结论；

②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形，取AB的中点P，求得P（-，0），得到PA=PC=PB=，过D作x轴的平行线交y轴于R，交AC的延线于G，∠DCF=2∠BAC=∠DGC+∠CDG，解直角三角形即可得到结论．

解：（1）根据题意得A（-4，0），C（0，2），

∵抛物线y=-x2+bx+c经过A．C两点，

∴，

∴，

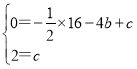抛物线解析式为： ;

（2）①令，

∴

解得： ,

∴B（1，0）

过点D作轴交AC于M，过点B作轴交AC于点N，

∴∥

∴

∴

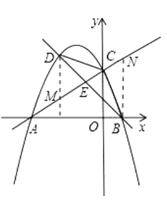
设：

∴

∵

∴

∴

∴当时，的最大值是 ;

②∵A（-4，0），B（1，0），C（0，2），

∴AC=2，BC=，AB=5，

∴AC2+BC2=AB2，

∴△ABC是以∠ACB为直角的直角三角形，

取AB的中点P，

∴P（-，0），

∴PA=PC=PB=，

∴∠CPO=2∠BAC，

∴tan∠CPO=tan（2∠BAC）=，

过D作x轴的平行线交y轴于R，交AC的延长线于G，如图，

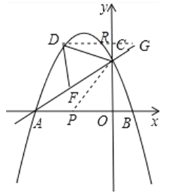
∴∠DCF=2∠BAC=∠DGC+∠CDG，

∴∠CDG=∠BAC，

∴tan∠CDG=tan∠BAC=，

即RC：DR=，

令D（a，-a2-a+2），

∴DR=-a，RC=-a2-a，

∴（-a2-a）：（-a）=1：2，

∴a1=0（舍去），a2=-2，

∴xD=-2，

∴-a2-a+2=3,

∴点D的坐标是