题目内容
【题目】计算下列各题
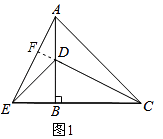
(1)如图1,△ABC和△E中,AB=CB,DB=EB,∠ABC=∠DBE=90°,D点在AB上,连接AE、DC.则AE和CD有什么数量和位置关系? 
(2)类比: 若将图1中的△DBE绕点B逆时针旋转一个锐角,如图2所示,问图2中的线段AE,CD之间的数量和位置关系还成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】
(1)解:AE=CD,AE⊥CD,
理由:延长CD交AE于F,
在△AEB和△CDB中,
∵ 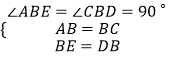 ,
,
∴△AEB≌△CDB(SAS)
∴AE=CD,
∠EAB=∠DCB,
∵∠DCB+∠CDB=90°,
∠ADF=∠CDB,
∴∠ADF+∠DAF=90°,
∴∠AFD=90°,
∴AE⊥CD
(2)解:解:(2)AE=CD,AE⊥CD,
∵∠DBE=∠ABC=90°,
∴∠ABE=∠DBC,
在△AEB和△CDB中, 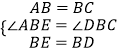
∴△AEB≌△CDB,
∴AE=CD,∠EAB=∠DCB,
∵∠DCB+∠COB=90°,∠AOK=∠COB,
∴∠KOA+∠KAO=90°,
∴∠AKC=90°,
∴AE⊥CD.
【解析】(1)延长CD交AE于K,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,由于∠DCB+∠CDB=90°,于是得到结论;(2)由于∠DBE=∠ABC=90°,得到∠ABE=∠DBC,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,等量代换得到∠KOA+∠KAO=90°,于是得到结论.
【考点精析】掌握旋转的性质是解答本题的根本,需要知道①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目


