题目内容
【题目】如图,点E在等边△ABC的边BC上,BE=6,射线CD⊥BC于点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+PF的值最小时,BF=9,则AC为( )

A.14B.13C.12D.10
【答案】C
【解析】
作点E关于直线CD的对称点G,过G作GF⊥AB于F,交CD于P,
推出此时,EP+PF的值最小,由∠B=60°,∠BFG=90°,推出∠G=30°,从而推出BG=18,从而求出CE=CG=6,进一步即可求出AC的长度.
∵△ABC是等边三角形,
∴AC=BC,∠B=60°,
作点E关于直线CD的对称点G,过G作GF⊥AB于F,交CD于P,
则此时,EP+PF的值最小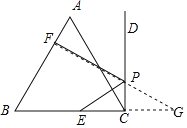 ,
,
∵∠B=60°,∠BFG=90°,
∴∠G=30°,
∵BF=9,
∴BG=2BF=18,
∴EG=12,
∵CE=CG=6,
∴AC=BC=12,
故选:C.

练习册系列答案
相关题目







