Question

【题目】函数的图象所示，若方程的解有四个不相等的实数根，则的取值范围是________．

Answer 1

【答案】

【解析】

根据二次函数y=ax2+bx+c（a≠0）与一元二次方程ax2+bx+c=0（a≠0）之间的关系可知，当y=0时，可得ax2+bx+c=0，则可根据方程的根的情况来判断抛物线与x轴的相交情况，若ax2+bx+c=0有解，则方程的解则对应抛物线与x轴交点的横坐标．那么方程|ax2+bx+c|=k的解有四个不相等的实数根，则说明函数y=|ax2+bx+c|（a≠0）与直线y=k有四个交点，结合图象即可求出k的取值范围．

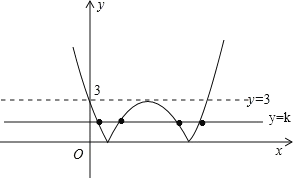
函数y=|ax2+bx+c|(a≠0)中当y=k时,即有|ax2+bx+c|=k,若方程|ax2+bx+c|=k的解有四个不相等的实数根,则说明函数y=|ax2+bx+c|(a≠0)与直线y=k有四个交点，如图，所以直线y=k应该在直线y=3和直线y=0之间，故k的取值范围为：0<k<3.

故答案为：0<k<3.