题目内容
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】解:(1)![]() 。
。
(2)△ABE为等边三角形。证明如下:
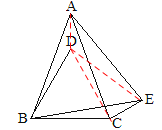
连接AD,CD,ED,
∵线段BC绕点B逆时针旋转![]() 得到线段BD,
得到线段BD,
∴BC=BD,∠DBC=60°。
又∵∠ABE=60°,
∴![]() 且△BCD为等边三角形。
且△BCD为等边三角形。
在△ABD与△ACD中,∵AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD(SSS)。∴![]() 。
。
∵∠BCE=150°,∴![]() 。∴
。∴![]() 。
。
在△ABD和△EBC中,∵![]() ,
,![]() ,BC=BD,
,BC=BD,
∴△ABD≌△EBC(AAS)。∴AB=BE。
∴△ABE为等边三角形。
(3)∵∠BCD=60°,∠BCE=150°,∴![]() 。
。
又∵∠DEC=45°,∴△DCE为等腰直角三角形。
∴DC=CE=BC。
∵∠BCE=150°,∴![]() 。
。
而![]() 。∴
。∴![]() 。
。
(1)∵AB=AC,∠BAC=![]() ,∴
,∴![]() 。
。
∵将线段BC绕点B逆时针旋转60°得到线段BD,∴![]() 。
。
∴![]() 。
。
(2)由SSS证明△ABD≌△ACD,由AAS证明△ABD≌△EBC,即可根据有一个角等于![]() 的等腰三角
的等腰三角
形是等边三角形的判定得出结论。
(3)通过证明△DCE为等腰直角三角形得出![]() ,由(1)
,由(1)![]() ,从
,从
而![]() ,解之即可。
,解之即可。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





