题目内容
【题目】背景材料:
在学习全等三角形知识时,数学兴趣小组发现这样一个模型,它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们知道这种模型称为手拉手模型.
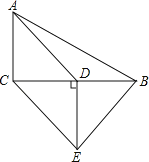
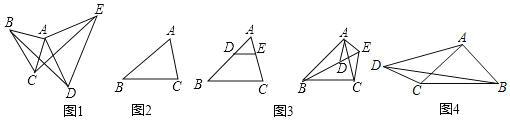
例如:如图1,两个等腰直角三角形△ABC和△ADE,∠BAC=∠EAD=90°,AB=AC,AE=AD,如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是手拉手模型,在这个模型中易得到△ABD≌△ACE.
学习小组继续探究:
(1)如图2,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,请作出一个手拉手图形(尺规作图,不写作法,保留作图痕迹),并连接BE,CD,证明BE=CD;
(2)小刚同学发现,不等腰的三角形也可得到手拉手模型,例如,在△ABC中AB>AC,DE∥BC,将三角形ADE旋转一定的角度(如图3),连接CE和BD,证明△ABD∽△ACE.
学以致用:
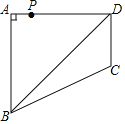
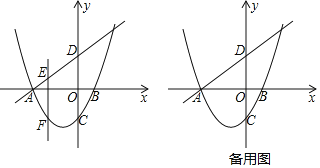
(3)如图4,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα=![]() ,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
【答案】(1)作图见解析,证明见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由等边三角形的性质可得AD=AB,AC=AE,∠DAB=∠EAC=60°,可得∠DAC=∠BAE,即可证△DAC≌△BAE,可得BD=CE;
(2)通过证明△ADE∽△ABC,可得![]() ,由旋转的性质可得∠BAC=∠DAE,即可得结论;
,由旋转的性质可得∠BAC=∠DAE,即可得结论;
(3)过点A 作AE垂直于AD,作∠AED=α,连接CE,则∠EDC=90°,通过证明△AEC∽△ADB,可得![]() ,由锐角三角函数和勾股定理可求AE,DE,EC的长,即可求BD的长.
,由锐角三角函数和勾股定理可求AE,DE,EC的长,即可求BD的长.
(1)作图
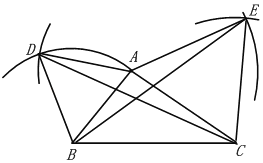
∵△ABD和△ACE都是等边三角形
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,且AD=AB,AC=AE
∴△DAC≌△BAE(SAS)
∴BE=CD
(2)如图,
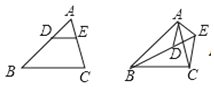
在第一个图中,∵DE∥BC
∴△ADE∽△ABC
∴![]()
∵将三角形ADE旋转一定的角度
∴∠BAC=∠DAE
∴∠BAD=∠CAE,且![]()
∴△ABD∽△ACE;
(3)如图,过点A 作AE垂直于AD,作∠AED=α,连接CE,则∠EDC=90°,
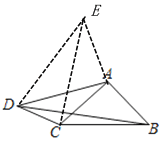
∵∠AED=∠ACB=α,∠CAB=∠DAE=90°
∴△AED∽△ACB
∴![]()
∵∠CAB=∠DAE=90°
∴∠CAE=∠DAB,且![]()
∴△AEC∽△ADB
∴![]()
∵△AED∽△ACB
∴∠ADE=∠ABC
∵∠ACB+∠ABC=90°,∠ADC=∠ACB
∴∠ADC+∠ADE=90°
∴∠EDC=90°
∵tanα=![]() ,AD=12.
,AD=12.
∴AE=16
∴DE=![]() =20
=20
∴EC=![]()
∵![]()
∴BD=![]()

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案