题目内容
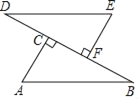
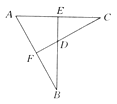
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.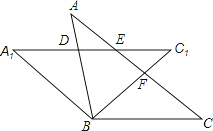
(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由.
【答案】
(1)
证明:∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C,
∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,
∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,
在△BCF与△BA1D中,
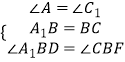 ,
,
∴△BCF≌△BA1D
(2)
解:四边形A1BCE是菱形,
∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,
∴∠A1=∠A,
∵∠ADE=∠A1DB,
∴∠AED=∠A1BD=α,
∴∠DEC=180°﹣α,
∵∠C=α,
∴∠A1=α,
∴∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,
∴∠A1=∠C,∠A1BC=∠AEC,
∴四边形A1BCE是平行四边形,
∴A1B=BC,
∴四边形A1BCE是菱形
【解析】(1)根据等腰三角形的性质得到AB=BC,∠A=∠C,由旋转的性质得到A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1 , 根据全等三角形的判定定理得到△BCF≌△BA1D;(2)由旋转的性质得到∠A1=∠A,根据平角的定义得到∠DEC=180°﹣α,根据四边形的内角和得到∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,证得四边形A1BCE是平行四边形,由于A1B=BC,即可得到四边形A1BCE是菱形.本题考查了旋转的性质,全等三角形的判定和性质,等腰三角形的性质,正确的理解题意是解题的关键.
【考点精析】关于本题考查的等腰三角形的性质和旋转的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.