题目内容
【题目】我们约定:对角线相等的四边形称之为:“等线四边形”。
(1)①在“平行四边形、菱形、矩形、正方形”中一定是“等线四边形”的是___________________;
②如图1,若四边形![]() 是“等线四边形”,
是“等线四边形”, ![]() 分别是边
分别是边![]() 的中点,依次连接
的中点,依次连接![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状:______________________;
的形状:______________________;
(2)如图2,在平面直角坐标系![]() 中,已知
中,已知![]() ,以
,以![]() 为直径作圆,该圆与
为直径作圆,该圆与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,若
,若![]() 为坐标系中一动点,且四边形
为坐标系中一动点,且四边形![]() 为“等线四边形”。当
为“等线四边形”。当![]() 的长度最短时,求经过
的长度最短时,求经过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)如图3,在平面直角坐标系![]() 中,四边形
中,四边形![]() 是“等线四边形”,
是“等线四边形”, ![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 在
在![]() 轴的负半轴上,且
轴的负半轴上,且![]() 。点
。点![]() 分别是一次函数
分别是一次函数![]() 与
与![]() 轴,
轴,![]() 轴的交点,动点
轴的交点,动点![]() 从点
从点![]() 开始沿
开始沿![]() 轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为
轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为![]() 秒,以
秒,以![]() 点为圆心,半径
点为圆心,半径![]() ,单位长度作圆,问:①当
,单位长度作圆,问:①当![]() 与直线
与直线![]() 初次相切时,求此时运动的时间
初次相切时,求此时运动的时间![]() ;②当运动的时间
;②当运动的时间![]() 满足
满足![]() 且
且![]() 时,
时,![]() 与直线
与直线![]() 相交于
相交于![]() ,求弦长
,求弦长![]() 的最大值。
的最大值。
【答案】(1)①矩形,正方形;②菱形;(2)![]() ;(3)①
;(3)①![]() ;②当
;②当![]() 时,
时,![]() 有最大值
有最大值![]()
【解析】
(1)①依据矩形,正方形的性质即可得出结论;②根据三角形中位线定理,菱形的判定定理可知它一定是菱形;
(2)连接CP,与圆相交于一点,当点Q在直线PC上时,PQ的长度为最短;利用勾股定理先求出C点坐标,再求出直线PC的方程,从而算出点Q的坐标,然后得到抛物线的解析式;
(3)根据题意可知点B、C坐标,设出点A、D坐标,由AD=![]() ,课求得A、D坐标,然后求得点P的坐标,再分别讨论BC与圆P的关系,从而求出时间;再求出弦MN的长度的最大值.
,课求得A、D坐标,然后求得点P的坐标,再分别讨论BC与圆P的关系,从而求出时间;再求出弦MN的长度的最大值.
解:(1)①在我们学习过的四边形中,矩形和正方形属于等对角线四边形;
故答案为;矩形,正方形.
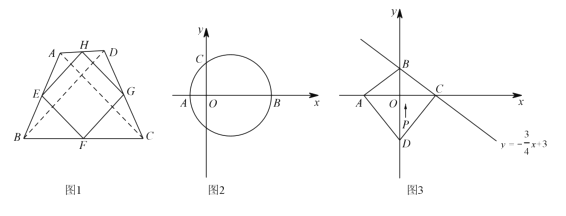
②如图,四边形ABCD是等线四边形,E、F、G、H分别是各边中点,
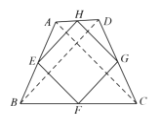
∵E、F、G、H分别是各边中点,
∴EF=GH=![]() ,EH=FG=
,EH=FG=![]() ,
,
∵AC=BD
∴EF=GH=EH=FG,
∴四边形EFGH是菱形.
(2)如图,连接CP与圆E相交于一点,连接CE,
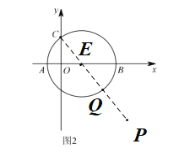
∵A(-2,0),B(8,0)
∴圆心![]() 坐标为
坐标为![]() ,
,![]() ,
,
∴![]() 中
中![]() ,
,
∴点![]() 坐标为
坐标为![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
∴圆心E(3,0)刚好在PC上.
当点![]() 在线段
在线段![]() 上时
上时![]() 最小,此时点Q在第四象限,
最小,此时点Q在第四象限,
∴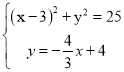 ,
,
解得:![]()
点![]() 坐标为
坐标为![]() ,
,
∴设过![]() 抛物线为
抛物线为![]() 则
则
![]() ,
,
∴![]() ;
;
(3)依题,如图
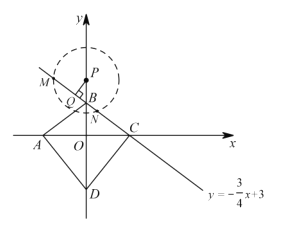
由直线方程令x=0,y=0可得,![]() 坐标分别为
坐标分别为![]() ,
,
设点![]() 坐标为
坐标为![]() ,
,
∵AC=BD,
∴点![]() 坐标为
坐标为![]() ,
,
∴![]() 中,
中,![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴点![]() 坐标分别为
坐标分别为![]() ,
,
∴点![]() 坐标为
坐标为![]() ;
;
①∴当![]() 与
与![]() 初次相切时
初次相切时![]() ,
,
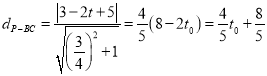
∴![]() ;
;
②当![]() 时,
时,![]() 逐渐增大,
逐渐增大,
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
当![]() 时,
时,![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
则![]()
∴![]()
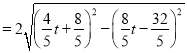
![]()
∴当![]() 时,
时,![]() 有最大值
有最大值![]() 。
。

 阅读快车系列答案
阅读快车系列答案