��Ŀ����
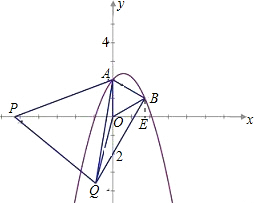
��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+2��ͼ����y�ύ�ڵ�A���Գ�����ֱ��x=
����OAΪ����y���Ҳ����ȱ�������OAB����Bǡ���ڸ��� �����ϣ� ����P��x���ϣ���PAΪ�����ȱ�������APQ����APQ�Ķ��� A��P��Q����ʱ���ǣ���
�����ϣ� ����P��x���ϣ���PAΪ�����ȱ�������APQ����APQ�Ķ��� A��P��Q����ʱ���ǣ���
��1�����B�������������ߵĽ���ʽ��
��2������P����ͼλ��ʱ����֤����APO�ա�AQB��
��3������P��x�����˶�ʱ����Q�պ����������ϣ����Q�����ꣻ
��4��̽�����Ƿ���ڵ�P��ʹ����A��O��Q��BΪ������ı��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
| ||
| 3 |
 �����ϣ� ����P��x���ϣ���PAΪ�����ȱ�������APQ����APQ�Ķ��� A��P��Q����ʱ���ǣ���
�����ϣ� ����P��x���ϣ���PAΪ�����ȱ�������APQ����APQ�Ķ��� A��P��Q����ʱ���ǣ�����1�����B�������������ߵĽ���ʽ��
��2������P����ͼλ��ʱ����֤����APO�ա�AQB��
��3������P��x�����˶�ʱ����Q�պ����������ϣ����Q�����ꣻ
��4��̽�����Ƿ���ڵ�P��ʹ����A��O��Q��BΪ������ı��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��������1�����ݺ�������ʽc=2���ɵó�OA=OB=AB=2������B��BE��x�����E������OB=2����AOB=60�㣬�����BE��OE�ij��ȣ��̶��ó���B�����꣬���ݺ����ĶԳ���Ϊx=
���ٽ���B���������ɵó���������ʽ��
��2�����ݵȱ������ε����ʿɵó�AB=AO��AP=AQ����PAO=��QAB������SAS��֤�ý��ۣ�
��3����Ҫ������������ٵ�Q�ڵ��������������ϣ��ڵ�Q�ڵ�һ�����������ϣ��ֱ���⼴�ɣ�
��4���ٵ���P��x�Ḻ������ʱ����Q�ڵ�B���·�����ʱ��AB��OQ���ڵ���P��x����������ʱ����Q�ڵ�B���Ϸ���ʱ��AQ��OB����������P�����꼴�ɣ�
| ||
| 3 |
��2�����ݵȱ������ε����ʿɵó�AB=AO��AP=AQ����PAO=��QAB������SAS��֤�ý��ۣ�
��3����Ҫ������������ٵ�Q�ڵ��������������ϣ��ڵ�Q�ڵ�һ�����������ϣ��ֱ���⼴�ɣ�
��4���ٵ���P��x�Ḻ������ʱ����Q�ڵ�B���·�����ʱ��AB��OQ���ڵ���P��x����������ʱ����Q�ڵ�B���Ϸ���ʱ��AQ��OB����������P�����꼴�ɣ�
����⣺��1������B��BE��x�����E��
�߶��κ�������ʽc=2��
��OA=OB=AB=2��
�֡�BOE=90��-��AOB=30�㣬
��BE=1��OE=
��
���B��������
��1����
����B�������ɵã�3a+
b+2=1�٣�
�Գ���=-
=
��
�����٢ڿɵ�a=-1��b=
��
�ʿɵú�������ʽΪ��y=-x2+
x+2��
��2��������ã�AB=AO��AP=AQ��
�֡ߡ�PAQ+��QOA=��BAO+��QAO��
���PAO=��QAB��
�ʿɵã���APO�ա�AQB��SAS����
��3���ٵ�Q�ڵ��������������ϣ���BQ��y�ύ��ΪF��
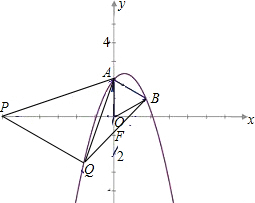
�ɣ�2���ɵá�ABQ=90�㣬
�֡ߡ�BAO=60�㣬
���QBO=30�㣬
��AFB=��AOB-��QBO=30�㣬
��AF=2AB=4��OF=2����F��0��-2��
��F��0��-2����B��
��1������y=kx+b��k=
��b=-2��
��ֱ��BQ����ʽΪ��y=
x-2��
�ⷽ���飺
��
��ã�
��
����ȥ��
�ʿɵõ�Q������Ϊ��-
��-6����
�ڵ�Q��B�غ�ʱ��Q������Ϊ��
��1��
�����������ĵ�Q����Ϊ����-
��-6������
��1����
��4���ɣ�2����֪����Q���ڹ���B����AB��ֱ��ֱ���ϣ��ɼ�AO��BQ��ƽ�У�
�ٵ���P��x�Ḻ������ʱ����Q�ڵ�B���·�����ʱ����AB��OQ���ı���AOQB�������Σ�
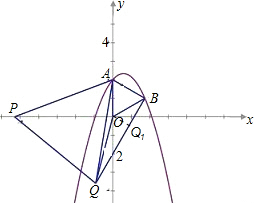
���P������Ϊx��
�ߡ�OBQ1=30�㣨����������˵������OB=2��
��OQ1=1��
���Q��������
��-
����
��AQ1=
=AP=
��
��ã�x=-
��
����ȥ����
�ڵ���P��x����������ʱ����Q�ڵ�B���Ϸ���ʱ����AQ��OB���ı���AOQB�������Σ�
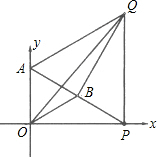
�ߡ�APO=30�㣬AO=2��
��OP=2
������P��������2
��0����
���Ͽɵ�P������Ϊ��-
��0����2
��0��

�߶��κ�������ʽc=2��
��OA=OB=AB=2��
�֡�BOE=90��-��AOB=30�㣬
��BE=1��OE=
| 3 |
���B��������
| 3 |
����B�������ɵã�3a+
| 3 |
�Գ���=-
| b |
| 2a |
| ||
| 3 |
�����٢ڿɵ�a=-1��b=
2
| ||
| 3 |
�ʿɵú�������ʽΪ��y=-x2+
2
| ||
| 3 |
��2��������ã�AB=AO��AP=AQ��
�֡ߡ�PAQ+��QOA=��BAO+��QAO��
���PAO=��QAB��
�ʿɵã���APO�ա�AQB��SAS����
��3���ٵ�Q�ڵ��������������ϣ���BQ��y�ύ��ΪF��

�ɣ�2���ɵá�ABQ=90�㣬
�֡ߡ�BAO=60�㣬
���QBO=30�㣬
��AFB=��AOB-��QBO=30�㣬
��AF=2AB=4��OF=2����F��0��-2��
��F��0��-2����B��
| 3 |
| 3 |
��ֱ��BQ����ʽΪ��y=
| 3 |
�ⷽ���飺
|
��ã�
|
|
�ʿɵõ�Q������Ϊ��-
4
| ||
| 3 |
�ڵ�Q��B�غ�ʱ��Q������Ϊ��
| 3 |
�����������ĵ�Q����Ϊ����-
4
| ||
| 3 |
| 3 |
��4���ɣ�2����֪����Q���ڹ���B����AB��ֱ��ֱ���ϣ��ɼ�AO��BQ��ƽ�У�
�ٵ���P��x�Ḻ������ʱ����Q�ڵ�B���·�����ʱ����AB��OQ���ı���AOQB�������Σ�

���P������Ϊx��
�ߡ�OBQ1=30�㣨����������˵������OB=2��
��OQ1=1��
���Q��������
| ||
| 2 |
| 1 |
| 2 |
��AQ1=
(0-
|
| (0-x)2+(2-0)2 |
��ã�x=-
| 3 |
| 3 |
�ڵ���P��x����������ʱ����Q�ڵ�B���Ϸ���ʱ����AQ��OB���ı���AOQB�������Σ�

�ߡ�APO=30�㣬AO=2��
��OP=2
| 3 |
| 3 |
���Ͽɵ�P������Ϊ��-
| 3 |
| 3 |
���������⿼���˶��κ������ۺ��⣬�ۺϿ����֪ʶ��϶࣬ע���ڽ��ÿһ��ʱ��������ͼ�Σ����������Ƿ������Ҫ�����ǽ���ѧ֪ʶ���ڻ��ͨ��

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��