题目内容
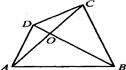 如图,△ABC,△BCD,△CDA的面积分别为49,27和14平方米,则△AOD的面积为
如图,△ABC,△BCD,△CDA的面积分别为49,27和14平方米,则△AOD的面积为
8
8
平方米.分析:设△ABO、△BCO、△COD、△DOC的面积分别为a、b、c、d,求出a+2b+2c+d=90,进而求出S△ABD=36,
然后求出S△ABD:S△BCD=4:3,利用同底等高的三角形面积相等求出S△AOD:S△COD=4:3,
再根据S△AOD+S△COD=14求出△AOD的面积.
然后求出S△ABD:S△BCD=4:3,利用同底等高的三角形面积相等求出S△AOD:S△COD=4:3,
再根据S△AOD+S△COD=14求出△AOD的面积.
解答: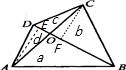 解:如图,作AE⊥BD,CF⊥BD.
解:如图,作AE⊥BD,CF⊥BD.
∵a+b=49,b+c=27,c+d=14,
∴a+2b+2c+d=49+27+14=90,
∴(a+b+c+d)+(b+c)=90,
即(a+b+c+d)+27=90,
a+b+c+d=63.
又∵b+c=27,
∴a+d=36,
∴S△ABD:S△BCD=36:27=4:3.
故AE:CF=4:3,
∴S△AOD:S△COD=4:3,
又∵S△AOD+S△COD=14,
∴S△AOD=8.
故答案为:8.
 解:如图,作AE⊥BD,CF⊥BD.
解:如图,作AE⊥BD,CF⊥BD.∵a+b=49,b+c=27,c+d=14,
∴a+2b+2c+d=49+27+14=90,
∴(a+b+c+d)+(b+c)=90,
即(a+b+c+d)+27=90,
a+b+c+d=63.
又∵b+c=27,
∴a+d=36,
∴S△ABD:S△BCD=36:27=4:3.
故AE:CF=4:3,
∴S△AOD:S△COD=4:3,
又∵S△AOD+S△COD=14,
∴S△AOD=8.
故答案为:8.
点评:此题考查了三角形的面积及等积变换,利用方程组解出三角形的面积并利用同底等高的三角形的面积相等解答.

练习册系列答案
相关题目
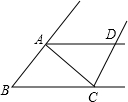 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
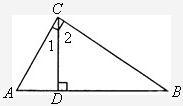
 ,且CB=CE.
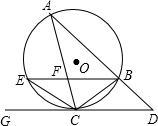
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.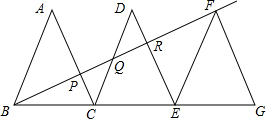 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且