题目内容
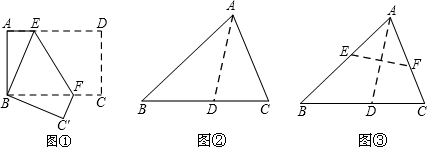
(1)动手操作:如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点c'处,折痕为EF,若∠ABE=20°,那么∠EFC'的度数为
(2)观察发现:
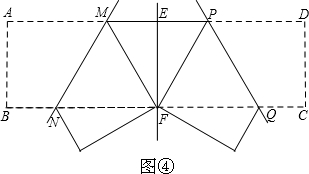
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
(3)实践与运用:
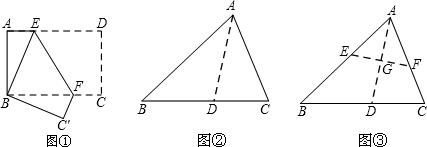
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.
分析:(1)根据直角三角形的两个锐角互余求得∠AEB=70°,根据折叠重合的角相等,得∠BEF=∠DEF=55°,根据平行线的性质得到∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°;
(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;
(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.
(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;
(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.
解答:解:(1)∵在直角三角形ABE中,∠ABE=20°,
∴∠AEB=70°,
∴∠BED=110°,
根据折叠重合的角相等,得∠BEF=∠DEF=55°.
∵AD∥BC,
∴∠EFC=125°,
再根据折叠的性质得到∠EFC′=∠EFC=125°.
故答案为125°;
(2)同意.
如图,设AD与EF交于点G.
由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
由折叠知,∠AGE=∠DGE=90°,
所以∠AGE=∠AGF=90°,
所以∠AEF=∠AFE.
所以AE=AF,
即△AEF为等腰三角形.
(3)由题意得出:
∠NMF=∠AMN=∠MNF,
∴MF=NF,由对称性可知,
MF=PF,
∴NF=PF,
而由题意得出:MP=MN,MF=MF,
在△MNF和△MPF中,
∵
,
∴△MNF≌△MPF(SSS),
∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,
即3∠MNF=180°,
∴∠MNF=60°,
∴∠AEB=70°,
∴∠BED=110°,
根据折叠重合的角相等,得∠BEF=∠DEF=55°.
∵AD∥BC,
∴∠EFC=125°,
再根据折叠的性质得到∠EFC′=∠EFC=125°.
故答案为125°;

(2)同意.
如图,设AD与EF交于点G.
由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
由折叠知,∠AGE=∠DGE=90°,
所以∠AGE=∠AGF=90°,
所以∠AEF=∠AFE.
所以AE=AF,
即△AEF为等腰三角形.
(3)由题意得出:

∠NMF=∠AMN=∠MNF,
∴MF=NF,由对称性可知,
MF=PF,
∴NF=PF,
而由题意得出:MP=MN,MF=MF,
在△MNF和△MPF中,
∵
|
∴△MNF≌△MPF(SSS),
∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,
即3∠MNF=180°,
∴∠MNF=60°,
点评:此题的综合性较强,综合运用了折叠的性质、等边三角形的性质以及勾股定理.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

 动手操作
动手操作 动手操作:如图,在10×10的正方形网格中,有一矩形ABCD.
动手操作:如图,在10×10的正方形网格中,有一矩形ABCD. 动手操作:如图,在10×10的正方形单位网格中,有一矩形ABCD.
动手操作:如图,在10×10的正方形单位网格中,有一矩形ABCD. 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.