题目内容
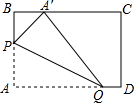 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.求:(1)当点Q与点D重合时,A′C的长是多少?
(2)点A′在BC边上可移动的最大距离是多少?
分析:(1)画出图形,根据折叠的性质得出A1'D=AD=5,在RT△A1DC中利用勾股定理即可得出答案.
(2)找出两个极值点的位置,然后即可判断点A'的移动范围,继而可得出答案.
(2)找出两个极值点的位置,然后即可判断点A'的移动范围,继而可得出答案.
解答:解:(1)当Q点与D重合时,如图①,
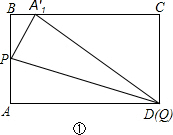
∵四边形ABCD是矩形,AD=5,AB=3,
∴BC=AD=5,DC=AB=3,∠C=90°,
由折叠知A1'D=AD=5,
在Rt△A1CD中,根据勾股定理,得A1'C2+DC2=A1'D2,A1'C2=A1'D2-DC2=52-32=16,
∵A1'C>0,
∴A1'C=
=4;
(2)

A'在BC上最左边时点Q点与D重合,此时,由(1)得,A'C=4,
当点P与B重合时,图②中的A'2在BC上最右边,
此时,由折叠知:A'2B=AB=3,则A'2C=5-3=2,A'应在A'1、A'2之间移动,
∴A'在BC边上可移动的最大距离为CA'1-CA'2=4-2=2.

∵四边形ABCD是矩形,AD=5,AB=3,
∴BC=AD=5,DC=AB=3,∠C=90°,
由折叠知A1'D=AD=5,
在Rt△A1CD中,根据勾股定理,得A1'C2+DC2=A1'D2,A1'C2=A1'D2-DC2=52-32=16,
∵A1'C>0,
∴A1'C=
| 16 |
(2)

A'在BC上最左边时点Q点与D重合,此时,由(1)得,A'C=4,
当点P与B重合时,图②中的A'2在BC上最右边,
此时,由折叠知:A'2B=AB=3,则A'2C=5-3=2,A'应在A'1、A'2之间移动,
∴A'在BC边上可移动的最大距离为CA'1-CA'2=4-2=2.
点评:本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象造成错误.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
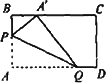
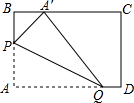 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
