题目内容
如图是一个形如正六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,…,依此类推.

(1)填写下表:
(2)写出第n层所对应的点数(n≥2);
(3)写出n层的正六边形点阵的总点数(n≥2);
(4)如果点阵中所有层的总点数为331,请求出它共有几层?

(1)填写下表:
| 层数 | 1 | 2 | 3 | 4 | … |
| 该层对应的点数 | 1 | 6 | 12 | 18 | … |
| 所有层的总点数 | 1 | | | | … |
(3)写出n层的正六边形点阵的总点数(n≥2);
(4)如果点阵中所有层的总点数为331,请求出它共有几层?
(1)7、19、37;(2)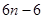 ;(3)
;(3)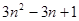 ;(4)11层
;(4)11层
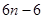 ;(3)
;(3)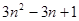 ;(4)11层
;(4)11层试题分析:根据六边形有六条边,则第一层有1个点,第二层有2×6-6=6(个)点,第三层有3×6-6=12(个)点,根据这个特征得到规律,再把这个规律应用于解题即可.
(1)第一层上的点数为1;
第二层上的点数为6=1×6;
第三层上的点数为6+6=2×6;
第四层上的点数为6+6+6=3×6;
…
第n层上的点数为(n-1)×6;
则2层六边形点阵的总点数为1+6=7
3层六边形点阵的总点数为1+6+12=19
4层六边形点阵的总点数为1+6+12+18=37;
(2)n层六边形点阵的总点数为1+1×6+2×6+3×6+…+(n-1)×6
=1+6[1+2+3+4+…+(n-1)]=1+6[(1+2+3+…+n-1)+(n-1+n-2+…+3+2+1)]÷2
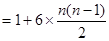
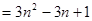 ;
;(3)由题意得
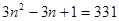
解得
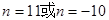 (舍去)
(舍去)答:共有11层.
点评:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
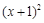
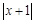
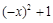
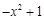


 ,
, ,求
,求 的值;
的值;
 =_______________.
=_______________. =
=  x-3
x-3 .
.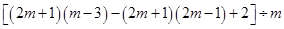 ,其中
,其中