题目内容
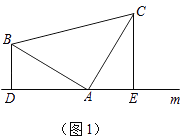
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N. 
(1)求证:MN=AM+BN.
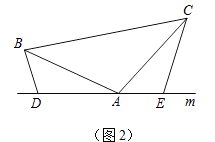
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.
【答案】
(1)证明:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
∠AMC=∠CNB,
∠MAC=∠NCB,
AC=CB,
△AMC≌△CNB(AAS),
AM=CN,MC=NB,
∵MN=NC+CM,
∴MN=AM+BN
(2)证明:结论:MN=BN﹣AM.
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
∠AMC=∠CNB,
∠MAC=∠NCB,
AC=CB,
△AMC≌△CNB(AAS),
AM=CN,MC=NB,
∵MN=CM﹣CN,
∴MN=BN﹣AM
【解析】(1)利用互余关系证明∠MAC=∠NCB,又∠AMC=∠CNB=90°,AC=BC,故可证△AMC≌△CNB,从而有AM=CN,MC=BN,利用线段的和差关系证明结论;(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目