题目内容
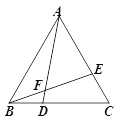
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.3cm
B.4cm
C.5cm
D.6cm
【答案】A
【解析】解:在Rt△ABC中,由勾股定理可知:AB= ![]() =
= ![]() =10,
=10,
由折叠的性质可知:DC=DE,AC=AE=6,∠DEA=∠C=90°,
∴BE=AB﹣AE=10﹣6=4,∠DEB=90°,
设DC=x,则BD=8﹣x,DE=x,
在Rt△BED中,由勾股定理得:BE2+DE2=BD2 ,
即42+x2=(8﹣x)2 ,
解得:x=3,
∴CD=3.
故选A.
利用勾股定理在Rt△ABC中求出AB的长,再根据折叠的性质得出DC=DE,AC=AE=6,∠DEA=∠C=90°,然后在Rt△BED中,利用勾股定理求出DE的长,就可得出CD的长。

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
【题目】某公司员工的月工资情况统计如下表:
员工人数 | 2 | 4 | 8 | 20 | 8 | 4 |
月工资(元) | 5000 | 4000 | 2000 | 1500 | 1000 | 700 |
(1)分别计算该公司员工月工资的平均数、中位数和众数;
(2)你认为用(1)中计算出的哪个数据来代表该公司员工的月工资水平更为合适?请简要说明理由.
【题目】甲、乙两人参加某网站的招聘测试,测试由网页制作和语言两个项目组成,他们各自的成绩(百分制)如下表所示:
应聘者 | 网页制作 | 语言 |
甲 | 80 | 70 |
乙 | 70 | 80 |
该网站根据成绩在两人之间录用了甲,则本次招聘测试中权重较大的是_____项目.