��Ŀ����
����Ŀ������⡣
��1����ͼ��1������֪���ڡ�ABC�У���BAC=90�㣬AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E��
֤����DE=BD+CE��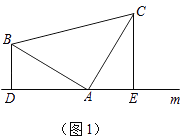
��2����ͼ��2��������1���е�������Ϊ���ڡ�ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ������С�BDA=��AEC=��BAC=�������Ц�Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ��������������������֤����������������˵�����ɣ� 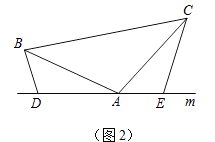
��3����չ��Ӧ�ã���ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�����FΪ��BACƽ�����ϵ�һ�㣬�ҡ�ABF�͡�ACF��Ϊ�ȱ������Σ�����BD��CE������BDA=��AEC=��BAC�����жϡ�DEF����״�� 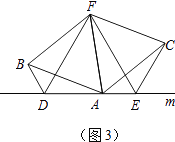
���𰸡�
��1��֤������BD��ֱ��m��CE��ֱ��m��
���BDA=��CEA=90�㣬
�ߡ�BAC=90�㣬
���BAD+��CAE=90�㣬
�ߡ�BAD+��ABD=90�㣬
���CAE=��ABD��
���ڡ�ADB�͡�CEA��
 ��
��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE
��2��֤����������
�ߡ�BDA=��BAC=����
���DBA+��BAD=��BAD+��CAE=180�㩁����
���CAE=��ABD��
���ڡ�ADB�͡�CEA��
 ��
��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE
��3��֤������DEF�ǵȱ������Σ�
�ɣ�2��֪����ADB�ա�CEA��
BD=AE����DBA=��CAE��
�ߡ�ABF�͡�ACF��Ϊ�ȱ������Σ�
���ABF=��CAF=60�㣬
���DBA+��ABF=��CAE+��CAF��
���DBF=��FAE��
��BF=AF
�ڡ�DBF�͡�EAF��
 ��
��
���DBF�ա�EAF��SAS����
��DF=EF����BFD=��AFE��
���DFE=��DFA+��AFE=��DFA+��BFD=60�㣬
���DEFΪ�ȱ�������
����������1������BD��ֱ��m��CE��ֱ��m�á�BDA=��CEA=90�㣬����BAC=90�㣬���ݵȽǵ������ȵá�CAE=��ABD��Ȼ����ݡ�AAS�����жϡ�ADB�ա�CEA��
��AE=BD��AD=CE������DE=AE+AD=BD+CE����2���루1����֤������һ������3����ǰ��Ľ��۵õ���ADB�ա�CEA����BD=AE����DBA=��CAE�����ݵȱ������ε����ʵá�ABF=��CAF=60�㣬���DBA+��ABF=��CAE+��CAF�����DBF=��FAE��
���á�SAS�����жϡ�DBF�ա�EAF������DF=EF����BFD=��AFE�����ǡ�DFE=��DFA+��AFE=��DFA+��BFD=60�㣬���ݵȱ������ε��ж������ɵõ���DEFΪ�ȱ������Σ�
�����㾫�������յȱ������ε��ж��ǽ����ĸ�������Ҫ֪�������Ƕ���ȵ��������ǵȱ������Σ���һ���ǵ���60��ĵ����������ǵȱ������Σ�

����Ŀ��ij��˾Ա�����¹������ͳ�����±���
Ա������ | 2 | 4 | 8 | 20 | 8 | 4 |
�¹��ʣ�Ԫ�� | 5000 | 4000 | 2000 | 1500 | 1000 | 700 |
��1���ֱ����ù�˾Ա���¹��ʵ�ƽ��������λ����������
��2������Ϊ�ã�1���м�������ĸ������������ù�˾Ա�����¹���ˮƽ��Ϊ���ʣ����Ҫ˵�����ɣ�

