题目内容
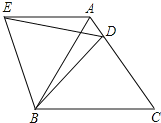
【题目】如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE.请说明EF平分∠AED.

【答案】见解析.
【解析】
先利用角平分线定义得到∠ABD=∠CBD,再根据平行线的性质由ED∥BC得∠EDB=∠CBD,则∠ABD=∠EDB,接着由∠FED=∠BDE可判断EF∥BD,则利用平行线的性质得∠EDB=∠DEF,∠ABD=∠AEF,所以∠AEF=∠DEF,从而得到结论.
∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线的定义).
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠BDE(等量代换).
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行),∠FED=∠ABD(等量代换),
∴∠AEF=∠ABD(两直线平行,同位角相等),
∴∠AEF=∠FED(等量代换),
∴EF平分∠AED(角平分线的定义).

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目