题目内容
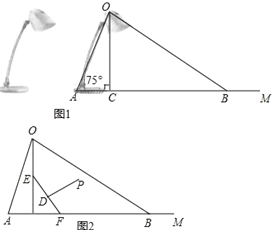
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.73)
≈1.73)
(1)求该台灯照亮水平桌面的宽度BC.
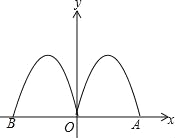
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.试问:最佳视点P在不在灯光照射范围内?并说明理由.
【答案】(1)83.9cm;(2)最佳视点P在灯光照射范围内.
【解析】
(1)在直角三角形ACO中,根据sin75°=![]() ,求出OC,在直角三角形BCO中,tan30°
,求出OC,在直角三角形BCO中,tan30°![]() 求出BC即可.
求出BC即可.
(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,延长HP交BO于T,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°,求出PH,TH的长即可判断.
解:(1)在直角三角形ACO中,sin75°=![]() ,
,
解得OC=50×0.97≈48.5,
在直角三角形BCO中,tan30°![]()
解得BC=1.73×48.5≈83.9.
答:该台灯照亮水平面的宽度BC大约是83.9cm.
(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,延长HP交BO于T,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°
由题意DE=DF=12,DP=34,
∴![]()
∴![]()
又∵![]()
∴HB=CB﹣CH=83.9﹣35.41≈48.49,
∵∠OBC=30°,tan∠OBC![]()
∴![]()
∵27.38<28.03
∴最佳视点P在灯光照射范围内.

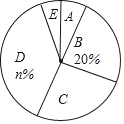
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 | m | 54 | 9 |
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %.
(2)被调查学生的总人数为 人,统计表中m的值为 ,统计图中n的值为 ;
(3)在统计图中,B类所对应扇形圆心角的度数为 ;
(4)该校共有1000名学生,根据调查结果,估计该校最喜爱A类节目的人数.